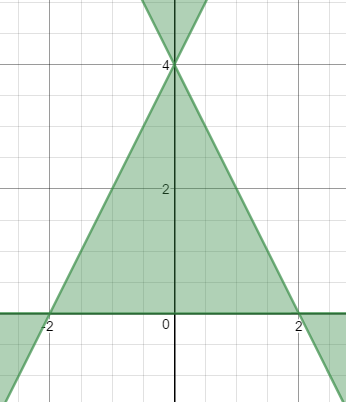
A follow-up question from this year's Christmas Graph Post: "You said we should be able to factor equation T (the Christmas tree outline equation). How?" - Kevin from Nebraska

Hi Kevin, first of all, for anyone who doesn't want to go find the equation in the other post, here it is:

Let T be the equation: 4x²y - y³ + 8y² - 16y ≤ 0

The first step in factoring this should be easy; every term on the left has a y in it, so we can factor that out:

y(4x² - y² + 8y - 16)

The next step is to split 4x² - y² + 8y - 16 into groups, in the hope that we can find a grouping that will help us factor it further. Grouping is not always a cut-and-dried process; sometimes it's easy to find a grouping that helps, sometimes it's hard. And, of course, sometimes it's impossible, which makes the process both frustrating (when you can't find a grouping that works) and satisfying (when you do!).

Typically, if I have four terms, the first thing I try is to split it into pairs, and factor each of the pairs:

(4x² - y²) + (8y - 16)
(2x - y)(2x + y) + 8(y - 2)

If the (y - 2) on the right matched either of the binomials on the left, we'd be able to factor this some more. Alas, no such luck. Let's try another grouping:

(4x² -16) - (y² - 8y)
4(x - 2)(x + 2) - y(y - 8)

Still no joy. Let's try another grouping:

(4x² + 8y) - (y² +16)

This one is also useless, because we can't factor the second group at all. At this point, I start re-evaluating my method; maybe grouping in pairs isn't the right way to go. Maybe I should create groups that are mismatched in size. For example:

4x² - (y² - 8y + 16) 

Suddenly, I realize, "Hey! That thing in the parentheses is a perfect square!"

4x² - (y - 4)² 

Wonderful! This is a difference of squares!

[2x + (y - 4)][2x - (y - 4)]
(2x + y - 4)(2x - y + 4)

So the full factorization is:

y(2x + y - 4)(2x - y + 4) ≤ 0

Now you can go back to the page for the Christmas tree graph and see why this graphs as shown at the top of this post.

Merry Christmas from me and my four year old son. Here's a Christmas tree ornament we built this morning. Each face is a triangle, and there are twenty faces in all. The faces are all made from last year's Christmas cards, cut into circles, and then folded around the shape of an equilateral triangle, in order to simultaneously form the face and provide a surface for gluing. Click the image for a larger view.

The icosahedron is one of 5 Platonic solids (regular solids). The complete list is:

• Tetrahedron: Four sides that are all equilateral triangles
• Cube: Six sides that are all squares
• Octahedron: Eight sides that are all equilateral triangles
• Dodecahedron: Twelve sides that are all regular pentagons
• Icosahedron: Twenty sides that are all equilateral triangles

I've made ornaments/decorations from three of those five shapes; maybe when I've done all five I'll publish an instruction sheet for each!

Merry Christmas! 

I was up at 3:30 AM today, so I decided to create a Christmas graph for all of my friends. This graph is made up of several inequalities combined with  ∩ (intersection) and  ∪ (union), and I hope you'll stick with me to the end to see what it looks like. Are you ready?

Let B be the equation: y² + 0.5y ≤ 0; {-0.5 ≤ x ≤ 0.5}

Let S be the equation: 81x⁴ - 18x²y² + 153x²y -326.25x² + y⁴ - 17y³ + 108.25y² - 306y + 324 ≥ 0 {-1/12 ≤ x ≤ 1/12}

Let C₁ be the equation: (x - 0.3)² + (y - 2.5)^2 - 0.0625 ≤ 0

Let T be the equation: 4x²y - y³ + 8y² - 16y ≤ 0

Let C₂ be the equation: x² + y² - 3y - 4 ≤ 0

Let O be the equation: [(x - .3)² + (y - 2.5)² - 0.02][(x - .3)² + (y - 2.5)² - 0.02][(x - .3)² + (y - 2.5)² - 0.02] ≥ 0

Let G be the equation: (y - .1 - .2(x - 1)²)(y - .2 - .2(x - 1)²)(y - 1.3 - .2(x - 1)²)(y - 1.4 - .2(x - 1)²)(y - 2.2 - .2(x - 1)²)(y - 2.3 - .2(x - 1)²)(y - 3.2 - .2(x - 1)²)(y - 3.3 - .2(x - 1)²) ≥ 0

Now graph the following:

B ∪ (S ∩ C₁) ∪ (T ∩ C₂ ∩ O ∩ G)

Okay, okay, this thing is ugly. I'm going to make it a little less ugly by factoring S, B, and T for you. You should be able to factor B and T on your own, but I'm certainly not going to ask anyone to factor S, so I'll just tell you how it factors. If you want to factor B and T on your own, take a moment to do so before reading further.

S factors into: (3x + y - 4.5)(3x - y + 4.5)(3x - y + 4)(3x + y -4) ≥ 0 {-1/12 ≤ x ≤ 1/12}

B factors into y(y + 0.5) ≤ 0; {-0.5 ≤ x ≤ 0.5}

T factors into:  y(2x + y - 4)(2x - y + 4) ≤ 0 (see the factoring process)

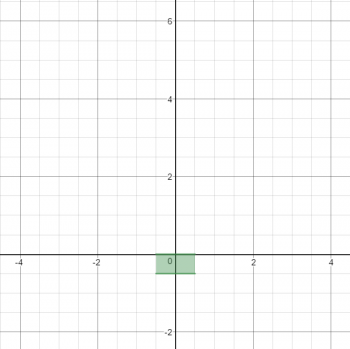
Let's begin by graphing the easiest part of this: B.

Since y(y + 0.5) ≤ 0, we can conclude that y must be between 0 and -0.5, so that the product of the two factors will be less than 0. However, we are also given the stipulation that x is between -0.5 and +0.5, which results in a simple box.

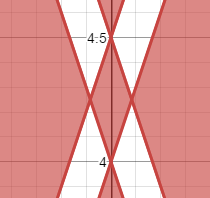
Now let's take a look at the intersection of S and C_1. S is a multiplication of four factors which are all linear, and they are in parallel pairs, which means this is going to be a parallelogram. Inside the parallelogram, two of the factors are negative and two are positive, which makes the whole thing positive. The graph looks like the picture to the right.

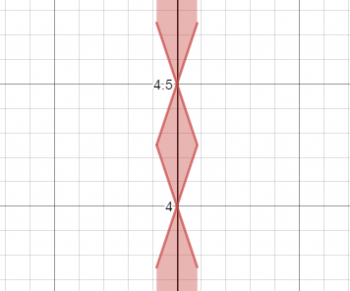
However, we have placed restrictions on the domain of this equation; x has to be between -0.5 and +05, which limits the graph as shown at the right.

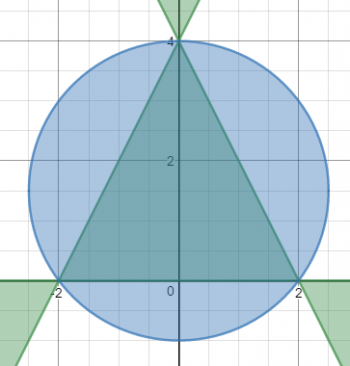
We still are not finished with this section of the graph; we have to intersect this with the equation C₁. This graph is a circle with center at (0, 4.25), and the interior of the circle is included. This further limits the graph to nothing but the rhombus.

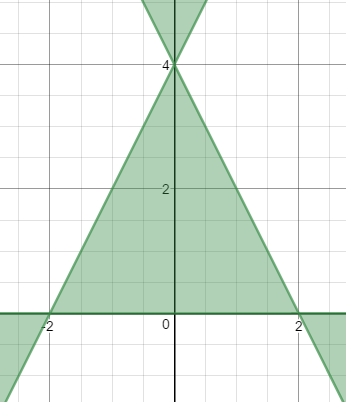
Okay, now the really challenging part. Equation T is very similar to equation S, except that instead of four factors, there are three. Thus, this contains a triangle, and since there are an odd number of factors, and they multiply to something less than or equal to zero, the interior of the triangle is included.

What's next? Well, in case you hadn't guessed C₂ is also a circle, and we're intersecting the interior of the circle with the triangle graph, which gives us the next graph.

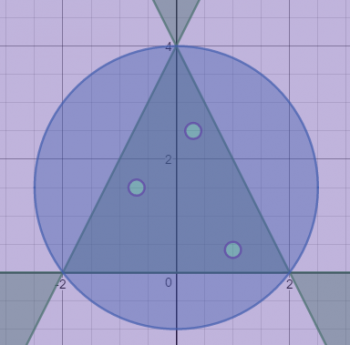
Then we have to deal with that hideous equation O, which appears to be...three circle factors multiplied together. If a point is on the interior of any of those three circles, that factor will be negative, and the other two will be positive, giving a negative result. However, equation O has the product greater than or equal to zero, which means that points satisfying O lie on or outside the three circles. The circles are all pretty small, and they're scattered around inside the triangle. Thus, we have the interior of a triangle, minus three circles, giving us the graph shown here.

What next? The even uglier equation G, which is a series of parabolas multiplied together as shown here.

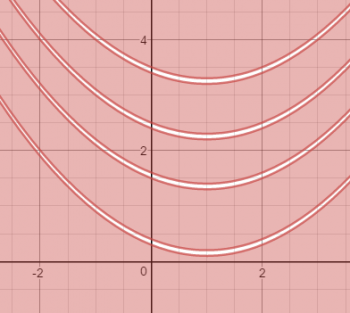
Now, if you were to take all of these and overlay them on top of one another, they would look something like this:

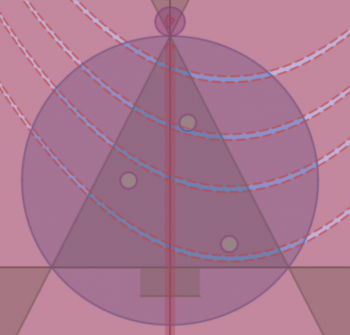
But...we're not overlaying them all; we have to take the intersection of T, C₂, O and G, and we also have to take the intersection of S and C₁. Then we overlay them (because it is a union of three separate graphs). I've shown them here with distinct colors for each of the three parts combined. Brown for the base (B), green for the tree (Tree ∩ Circle₂ ∩ Ornaments ∩  Garland), and yellow for the star (Star ∩ Circle₁).

Have a wonderful, Merry Christmas!
Professor Puzzler

P.S. Graph screen captures came from this graphing calculator.

Brock from Canada asks, "Computer programmers use hexadecimal code. I have read and learned your lesson on that but I cant figure out where to put and what the symbols mean when coding. these symbols are #,*,&. what do these symbols mean and where do I insert them when I am doing my programming?"

Hi Brock, thanks for your question. The answer is: it depends on the programming/scripting language you are using. Here are just a few examples. Note that in each example, the symbol (or symbols) that indicate a number is a hexadecimal value is shown in bold text.

If you were programming in the language C or C++, and you wanted to include a hexadecimal number in your program, it might look something like this:

int x = 0xFC;

If you were programming in Javascript your code would look the same.

If you were developing a website using HTML/CSS, and you wanted to provide a color as a hexadecimal value, it would look like this:

background-color:#FF0000;

This is equivalent to:

background-color:rgb(255,0,0);

If you were programming in PHP, you would also use 0x:

$x = 0xA3;

If you were programming in Visual Basic, you could write a hexadecimal number like this:

Dim x as Integer = &h2D

In Pascal (which I learned in college back in the 80s, but haven't used since), a hexadecimal value would be written with a dollar sign:

x := $B8;

Eighth grader Chase, from Canada, asks for examples of things that are horizontal.

Hi Chase,

It's funny that you should ask this question today, because when I was teaching my high school Physics class today, one of my students kept mixing up "horizontal" and "vertical." So before I give examples of horizontal, I thought I'd try to give everyone some helpful hints to remember the difference between horizontal and vertical.

If something is horizontal, that means it's lying down flat, and if it's vertical, it's standing up straight.

So how can you remember the difference? Well, I have two suggestions:

1. Remember that the horizon (the place far off in the distance where the land meets the sky) is flat. The horizon is horizontal. And no, it's not a coincidence that the word horizontal contains the word horizon!
2. Your vertebrae are the bones in your spine, and your spine stands up straight. Vertebrae, vertical. Both start with with "vert" and both are standing up straight.

So if you can remember one or the other of those things, you should be able to remember the difference between vertical and horizontal.

Okay, so now, to answer your question - what are some things that are horizontal?

• The horizon
• A table top
• A floor
• Roads (except on hills)
• The seat of a chair
• You, when you're sleeping! (and then your vertebrae aren't vertical!)

Some things that are vertical?

• Walls of most buildings
• Doors
• Cliffs
• Towers (except the leaning tower of Piza - that one is neither horizontal nor vertical!)
• Trees
• You, when you're standing up!