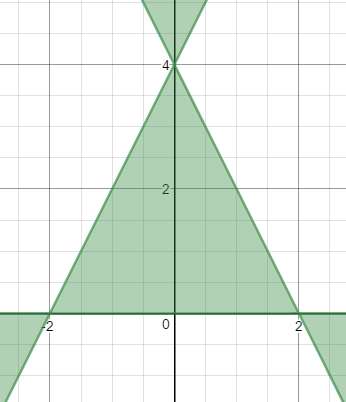
A follow-up question from this year's Christmas Graph Post: "You said we should be able to factor equation T (the Christmas tree outline equation). How?" - Kevin from Nebraska

Hi Kevin, first of all, for anyone who doesn't want to go find the equation in the other post, here it is:

Let T be the equation: 4x²y - y³ + 8y² - 16y ≤ 0

The first step in factoring this should be easy; every term on the left has a y in it, so we can factor that out:

y(4x² - y² + 8y - 16)

The next step is to split 4x² - y² + 8y - 16 into groups, in the hope that we can find a grouping that will help us factor it further. Grouping is not always a cut-and-dried process; sometimes it's easy to find a grouping that helps, sometimes it's hard. And, of course, sometimes it's impossible, which makes the process both frustrating (when you can't find a grouping that works) and satisfying (when you do!).

Typically, if I have four terms, the first thing I try is to split it into pairs, and factor each of the pairs:

(4x² - y²) + (8y - 16)
(2x - y)(2x + y) + 8(y - 2)

If the (y - 2) on the right matched either of the binomials on the left, we'd be able to factor this some more. Alas, no such luck. Let's try another grouping:

(4x² -16) - (y² - 8y)
4(x - 2)(x + 2) - y(y - 8)

Still no joy. Let's try another grouping:

(4x² + 8y) - (y² +16)

This one is also useless, because we can't factor the second group at all. At this point, I start re-evaluating my method; maybe grouping in pairs isn't the right way to go. Maybe I should create groups that are mismatched in size. For example:

4x² - (y² - 8y + 16) 

Suddenly, I realize, "Hey! That thing in the parentheses is a perfect square!"

4x² - (y - 4)² 

Wonderful! This is a difference of squares!

[2x + (y - 4)][2x - (y - 4)]
(2x + y - 4)(2x - y + 4)

So the full factorization is:

y(2x + y - 4)(2x - y + 4) ≤ 0

Now you can go back to the page for the Christmas tree graph and see why this graphs as shown at the top of this post.