Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
Martha asks, "Where does the phrase 'By the Seat of your Pants' come from?"
Well, Martha, I didn't know the answer to this one, so I checked a few different sources, and was able to piece together what seems like a reasonable explanation.
The one thing that all the sources agree on is that it's an old aviation expression. That makes sense, because the full phrase is typically "flying by the seat of your pants," even when the expression is being used in other contexts. For example, if you're playing volleyball, and you don't know how to serve, you wouldn't (probably) say "serving by the seat of my pants" you would still say "flying by the seat of my pants" even though you're not actually flying.
So where does this expression come from? What does it mean to "fly by the seat of your pants?"
Well, in the early days of aviation, the instruments for determining how fast you're going, what angle you're flying at, etc, were not very sophisticated, and in some cases either weren't installed in a plane, or malfunctioned in mid-flight. If that happened, you had to, in an almost literal sense, fly by the seat of your pants.
How would you know if your plane was declined from horizontal? Your "seat" started sliding forward in the pilot's chair. If you felt like you were going to land butt first on the floor, that was a pretty good indicator that you were on a pretty steep descent. Similarly, if you felt like your backside was getting pushed backward, it's a good bet that you're ascending.
What about banking? Well, if you've studied circular motion (or if you've just sat in a car taking a corner quickly!) you know that when the chair you're sitting in takes a corner, your body has a tendency to keep going in a straight line, until you start pressing up against the door, or the side of the chair. So if the plane is banking, you'll feel it in the seat of your pants, because you'll start sliding sideways in the chair.
So pilots who were very experienced could successfully fly a non-instrumented plane based solely on how their derriere was situated in the pilot's chair!
Today, it has taken a more idiomatic meaning. It simply means to do something without planning or organizing, or improvise. To put it another way, it's the same as "winging it," which - interestingly - is not an aviation metaphor. It's a theatrical metaphor, meaning that the person was doing last minute practicing in the stage wings (the offstage area where people waited before performing).
Flying by the seat of your pants. Winging it. Both mean to improvise, but they have vastly different origins!
First of all, I want to make it clear that not only am I not a bowling lane lubricant expert, I'm also not a bowling expert of any kind. I haven't been bowling in years. But your question reminded me of something that used to fascinate me as a teenager. We had a candlepin bowling place in town, and a group of teens from our church would often go there on a weekend evening to bowl.
There was an elderly little man named Harry who was always there. I used to watch him bowl with fascination. While everyone else was racing to the line and giving a powerful swing of the arm, little old Harry would waddle. I kid you not. It was almost painful to watch the snail's pace with which he would approach the line. And he was always holding the ball overhand instead of underhand like everyone else did. Basically he just walked up to the line with his arm hanging limply at his side.
And then, at the last moment, he'd give a flick of his wrist, and that ball would go skidding down the lane, and the pins would go flying. It was a strike every time. That little old man had perfect 300 score cards hung all over the walls of that place, and had won about every local bowling competition.
What was his secret? Well, I'm sure he had more than one, but here's one of Old Harry's secrets: backspin. Notice I said the ball skidded down the lane. Sure, it was rolling, but it was rolling backward, which meant it was really just floating in lane oil. What did that do for him? Consider the two images below.
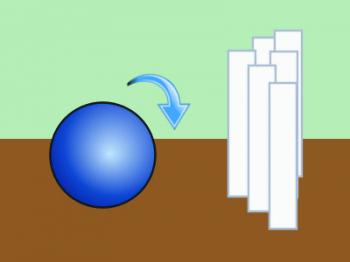
In the first image, we see a ball approaching the pins with a forward spin. You know what that ball is going to do to the pins? It's going to knock them down. But knocking pins down wasn't what happened when Old Harry was bowling. Take a look at the next picture, which shows a bowling ball approaching the pins with a reversed or back spin.
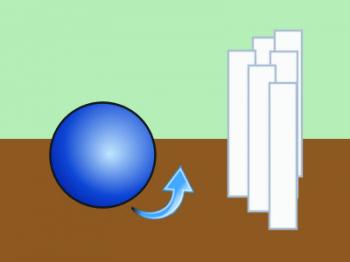
You know what that bowling ball is going to do? Sure, it's going to knock the pins over, but because of its spin direction, it was knocking those pins up. That backspin made the pins go flying everywhere. One pin flying upward would wreak a lot of havoc on the rest of the pins.
So what does this have to do with the lane lubricant? Simple. The lubricant lowers the coefficient of friction on the lane, which allows the ball to spin backward longer, before the spin slows to a stop and reverses to a forward spin (Try it sometime - send the ball down the lane with a backspin, and if the ball is multi-colored, you should be able to see the point at which it stops spinning backward and reverses to a forward spin). So if there was no oil on the lane, Old Harry's bowling ball would have reversed its spin before reaching the pins, and less havoc would have ensued.
And goodness knows, any time we can have havoc, we approve. :)
That coefficient of friction will also make a huge difference when it comes to sideways spins. Depending on how you release the ball, you can make the the ball do a nice "hook" at the last minute, and nail the pins at an angle. This is an important technique.
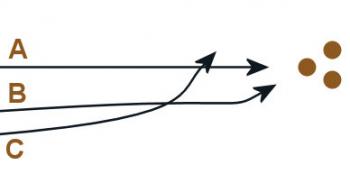
But when the ball hooks isn't just dependent on how you spin it; it's also dependent on the coefficient of friction. If there's no friction whatsoever (entirely theoretical - there's always friction), the spin will be completely irrelevant; the ball will go straight into the pins (line A). If the coefficient of friction is just right, the ball will do a combination of sliding and rolling, and hook at the very last moment (line B). Too much friction, and the hook happens too early, sending your ball careening into the gutter (line C).
But all of this depends on your having very good control of your release of the ball; for me, it was always a major accomplishment to have a frame without a gutter ball. Just a little piece of evidence that theoretical knowledge doesn't always give practical advantage!
Several months ago, Professor Puzzler wrote a blog post about the math problem "three over two x" (3/2x) and how it should be interpreted. The answer was: that's not a math problem; it's a typographical error, because fractions written with a diagonal bar, by typographical standards, should be written with the numerator a superscript, and the denominator a subscript, making it obvious whether the x is a part of the denominator, or separate from the fraction altogether.
A similar question has cropped up, and someone asked the Professor about how to interpret it: what is the answer when you perform the following operations:
6 ÷ 2(1 + 2)
This is another one of those facebook memes that people love to argue endlessly about. The primary arguments go as follows:
Argument #1
Do the parentheses first, giving you 6 ÷ 2 x 3. Now do the multiplication, giving: 6 ÷ 6. Now do the division and the answer is 1.
Argument #2
Do the parentheses first, giving you 6 ÷ 2 x 3. Now do the division, giving: 3 x 3. Now do the multiplication and the answer is 9.
Argument #3
Do the parentheses first, giving you 6 ÷ 2(3). Now do the parentheses (again), giving: 6 ÷ 6. Now do the division and the answer is 1.
Which of these arguments are valid?
Argument #1 is invalid, because once you're left with just division and multiplication, you do them from left to right. Multiplication does not take precedence over division! If you used argument #1, you should review BODMAS (PEMDAS).
Argument #2 is an acceptable argument. Here you're doing the multiplication and division from left to right, as required.
Argument #3 is also invalid, because "doing parentheses" means evaluating what's inside the parentheses, not combining them with things outside the parentheses.
Does that mean the answer is unequivocally 9? Or is there another argument to be made?
I'm going to stir the pot a little and suggest that there is another argument you could make.
Argument #4
BODMAS (PEMDAS) is a set of rules that is designed to tell us what to do with specific arithmetic operation graphemes*, and if we represent an arithmetic operation with a grapheme outside the set of graphemes, all bets are off.
* A grapheme is a visual, symbolic representation of something. For example, "A", "1", "÷" are all graphemes.
If you don't believe that using different graphemes can alter the order in which we do the problem, consider the following. Division can be represented by the symbol "÷" or by a vinculum (a horizontal fraction bar). With that in mind, are the following equivalent expressions?
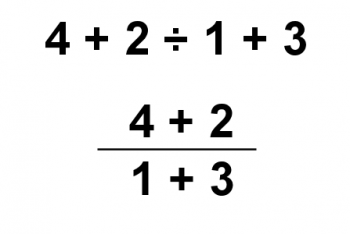
The answer is: of course they're not the same! The top expression is evaluated with 2 ÷ 1 calculated first, and then 4 + 2 + 3 = 9.
In the second expression, we evaluate the numerator and denominator first, giving 6 ÷ 4. Which gives 3/2 as the answer.
But they are both graphical representations of division! So why does the order of operations change? I tell my students that the vinculum is a "grouping symbol." In other words, it has implied parentheses. If you wanted to write it without the vinculum, you would have to add parentheses to the expression:
(4 + 2) ÷ (1 + 3)
Thus, even though the vinculum and "÷" are both division symbols, order of operations does not apply to them in exactly the same way.
In the same manner, one could argue that multiplication written with a different grapheme (in this case, the grapheme would be no grapheme at all) doesn't need to be interpreted in exactly the same way as multiplication written with the standard "x" grapheme. You could argue that in the same way that a vinculum as the division grapheme introduces implied parentheses into the problem, an empty grapheme for multiplication also introduces an implied grouping. In other words, 2(2 + 1) is actually an implied group: [2(2 + 1)]. This would change the answer to the original problem to 1 instead of 9.
And I would be hard pressed to provide a compelling argument against your interpretation, since I just got done telling you that a vinculum introduces an implied grouping!
Which leads us to the point I wanted to make from the beginning:
This is one of the reasons why, once we hit Algebra, we avoid using the ÷ grapheme for division. We almost entirely use a vinculum for division. Partly, that's because it allows us to be more compact in writing problems. But also because it becomes an implied grouping for division (allowing us to skip writing parentheses all over the place) AND it also avoids any chance of ambiguity that might arise from the question of how we write our multiplication. If a no-grapheme multiplication occurs under the vinculum, then it already has an implied grouping which it receives from the vinculum!
Veronica from Georgia asks, "A guy wants to buy a car and borrow $50,000. He gets $25,000 from his mom and $25,000 from his sister. He buys the car for $45,000. Driving home he runs into a friend that ask to borrow $3,000. You are now left with $2,000. You pay your mom and sister back $1,000 each and now you owe them only $24,000 each. After you pay them the $48,000 total to both, your friend pays you the $3000 he owes you. Do you know why the total comes out to $51,000 instead of $50,000 that you originally started out with?"
Hi Vernoica, This problem is very similar to the bellboy "missing dollar" problem, which you can read about by clicking the image below:

I'm going to use a slightly different approach in explaining this problem, by focusing on the meaning of positives and negatives in the context of transactions. Every financial transaction has a "direction." It is from one person (or organization/business, etc) and to another. We use positives and negatives to indicate the direction of a transaction. We should choose a single individual as the focus for our problem, and once we've done that, every transaction will be signed based on whether the transaction is TO or FROM that person. In this case, the choice is obvious: the guy buying the car is the focus.
So let's agree that if a monetary transaction has "the guy" as the recipient, we'll call that transaction positive. If "the guy" is the giver, we'll call it a negative transaction. So we can list every transaction as a signed number:
Recieves $25,000 from his mother: +$25,000
Receives $25,000 from his sister: +$25,000
Buys car for $45,000: -$45,000
Lends $3000: -$3,000
Pay mother $1,000: -$1,000
Pay sister: $1,000: -$1,000
Pay mother $24,000: -$24,000
Pay sister: $24,000: -$24,000
Friend pays back loan of $3,000: +$3,000
So now that we have all of these transactions signed, we can add them up properly:
$25,000 + $25,000 - $45,000 - $3,000 - $1,000 - $1,000 - $24,000 - $24,000 + $3,000 = -$45,000
What does that -$45,000 represent? It represents the amount by which "the guy" has decreased his bank balance (the price of the car).
What does the number $51,000 represent? Absolutely nothing. Whoever gave you the problem picked three transactions out of the list of nine transactions, gave one of them the incorrect sign, and then combined them in a way that makes absolutely no sense in the context of the problem. Why would that add up to anything interesting? You got fooled into thinking it should mean something because it was so close to $50,000, which was a number that was mentioned in the problem. But adding those three quantities means absolutely nothing. When you give the numbers the correct signs, all the transactions cancel out to a single transaction - the cost of the car.
Question: In your Gravity Train Simulator, you made the following statement: "If the train is inside the earth, the force of gravity acting on it is related not just to its distance from the center of the earth, but also on the amount of earth mass which is closer to the center of the earth than the train is." This seems to imply that all the mass outside the train's radius somehow cancels out. So if someone was in outer-space, inside an enormous steel shell - does that mean they would be weightless wherever they were in the shell? ~H. Borash
Answer: Yes, that's correct, H. To rigorously prove this, we would need to use a bit of Calculus, but I can show you a rough geometry approximation that'll help you see why it's true. First, a diagram. Here's a spherical shell. We'll assume it's absolutely enormous - big enough to enclose the earth and the sun. This hypothetical structure is called a Dyson sphere. I've marked the sun and the earth inside the sphere.
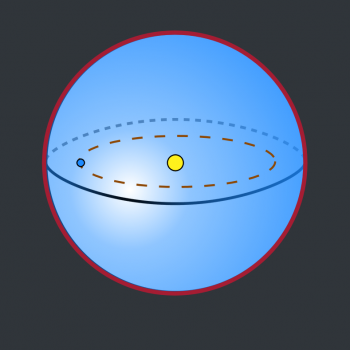
The yellow circle at the center of the sphere represents the sun, and the smaller blue circle to the left represents the earth. The brown dotted line represents the earth's orbit around the sun.
Obviously, this is not drawn to scale; it's difficult to make both the sun and earth to scale in a single diagram without the earth becoming nearly invisible. So I didn't even try.
But the question you asked is essentially equivalent to this: wouldn't the Dyson sphere throw the earth out of its orbit? That sphere has got to be incredibly massive, and planet earth is much closer to one side than the other. So wouldn't earth get dragged out of its orbit?
Or, to put it another way, if the sun wasn't there at all, and earth was motionless, would it stay motionless? Or would it get dragged toward the closer side of the sphere?
The answer to both questions is: No. No, the sphere would not drag the earth out of its orbit. No, earth would not go crashing into the sphere. All of the gravitational forces applied by the sphere on planet earth cancel each other out. Even though earth is not at the center of the sphere.
The reason is that because the earth is closer to one side, there is more mass on the other side, and the closeness of the mass on one side exactly cancels against the extra mass on the other side!
As I said above, a full, rigorous proof of this involves some Calculus, but I'm going to try to give you a non-calculus explanation that may help you visualize what's happening. I want to focus on two disks of the sphere - one close to the earth, and the other on the opposite side, furthest away from earth. To simplify, we're going to treat these as flat disks, so they don't exactly match the contour of the Dyson sphere:
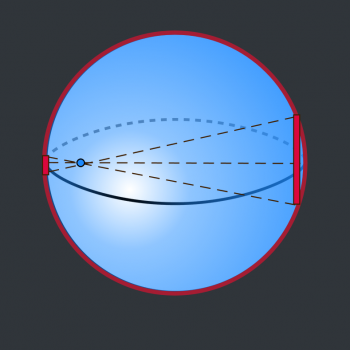
Notice how much bigger the disk on the right is, compared to the one on the left. That disk is much further away, so each cubic inch of that disk exerts less force on earth than a corresponding cubic inch of the closer disk.
On the other hand, you can easily see that the disk on the right contains many many more cubic inches than the disk on the left.
So maybe they cancel? Let's take a closer look.
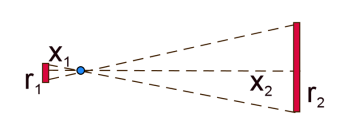
If we knew the thickness (h, for height) of the disk, as well as the density (D) of the material the disk is made of, we could calculate the masses (m1 and m2) of the two disks.
m1 = hπr12D
m2 = hπr22D
However, we have more variables than we need. Since we have some similar triangles, we can say that r2 = r1(x2/x1). This changes our second equation to: m2 = hπr12(x22/x12)D.
Now this is where the magic happens: we're going to plug both of those masses into the gravitational formula:
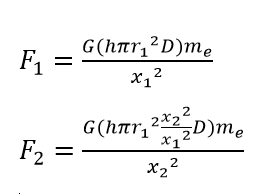
So even though one disk is much larger than the other, they both exert the same gravitational force on earth, canceling each other out!
Again, this is not a rigorous proof. Most proofs I've seen of this involve rings instead of disks, and doing integrals (calculus) to show that all the rings cancel. But this geometric demonstration hopefully helps you to see that it's a reasonable conclusion!

