The following picture (click it for a larger version) was seen on Facebook by my outlaw Jakob (his wife is my sister-in-law, which is why I refer to him as my outlaw). It was accompanied by the caption "Here Is The Reason Why 1 Is Called 1. , And 2 Is Called 2..."

Somehow, Jakob must have known that I would want to write a sarcastic, cynical post about this.

So let's start with the caption.

"Here Is The Reason Why 1 Is Called 1. , And 2 Is Called 2..."

Uh...no...your terminology is confused. "1" is not what the number is called; it's called "one." "1" is the grapheme for the number we call "one."

So I guess you meant to say "Here is the reason we use this grapheme for one, and that grapheme for two..."

Better?

No. Not at all. Historically, there is absolutely no reason to think that people invented their numerical graphemes based on the number of angles in the digits (mind you, there is some indication that various civilizations played with creating graphemes based on making the number of lines match the numeral being represented). Most of our digits went through a lengthy evolution process, and their original forms, like our modern forms, had far more curves than angles. Take the number three, for example. The number three has no angles at all. Neither does six, eight, or nine.

"Well sure," you might say, "but if you write it as a block numeral, with straight lines, then the grapheme for three has three angles."

Really? So why didn't you write zero that way? Because when I last checked, a zero has four angles when written in block form.

And let's face it, even if you want to write your numbers in block form, no one writes them like this. Check your calculator. A two is an inverted five, which means that, like five, it has four angles. Four. Not five. Not two. Four.

And that ridiculous looking seven? Some people put a hook at the top of their sevens. Some people put a line through the middle. But do you know anyone who puts a line at the bottom of their sevens? I've been teaching math for a long time, and I don't think I've ever seen anyone write a seven with that serif. Oh, and I just checked through all 150 fonts I have installed on my computer, and none of them have that. It's just silly.

Do we really even need to talk about that absurd nine? Who in the world puts a curl on the curl on the curl at the bottom of their nines?

I get to the end of their numbers and find myself wondering, "Why? Why?? Why does this thing even exist?"

I have no idea. Seriously.

It's not even a valuable mnemonic for remembering anything. It's purposeless. And on top of that, it has zero angels. What's up with that? Why even mention angels, if you're not going to include any?

As one commenter said, "I never looked at the digits this way before. And now I'm never going to do it again."

Thanks, outlaw!

Lately I've been getting a spate of questions about meter in poetry. These question range from "Is this poem iambic pentameter?" to "How do you tell if a syllable is stressed or not?"

Let's start with the second question: How do you tell if a syllable is stressed or not?

If it's trembling uncontrollably, or hiding under the blankets, it's probably a stressed syllable.

Okay, serious answer. A stressed syllable is a syllable that has emphasis within a word (or within a line of poetry). So the best way to tell is to say the word in an overly dramatic way, choosing different syllables to emphasize. For example, let's say we have the word "emphasize," and we want to figure out which syllable is stressed. So we try saying it a few different ways. Try reading the following line, and SHOUT whenever you see a capitalized syllable (or, if you're in a library, whisper when you see a lower-case syllable).

EM-pha-size, em-PHA-size, em-pha-SIZE.

Clearly the middle one sounds WRONG! So we know that the middle syllable is unstressed. But the first and last ones, neither of them sounds horrible, but EM-pha-size definitely sounds better than em-pha-SIZE. EM is the stressed syllable in the word, and the other two are unstressed.  You could argue that SIZE has a secondary stress, but the general rule is, only one syllable in a word has the primary stress.

When I was a little kid I could never say the word "aluminum" properly. Let's see if we can work it out by syllables. Get ready to SHOUT again!

A-lu-min-um, a-LU-min-um, a-lu-MIN-um, a-lu-min-UM.

Clearly the one that sounds correct is the second one. Thus, LU is the stressed syllable.

The interesting thing is that if you put multiple words together, we may start hearing some of those "secondary" stresses more clearly:

EM-pha-SIZE a-LU-min-UM.

Those two words sound really great together, because we hear it as alternating stressed and unstressed all the way through. If we switch the order, though, it doesn't sound right to say it that way:

a-LU-min-UM EM-pha-SIZE.

Somehow, those two stressed syllables next to each other sound awkward and cumbersome. However, if we let the UM and SIZE get "swallowed up" and treat them as unstressed syllables:

a-LU-min-um EM-pha-size.

Now it sounds more relaxed and natural. Read this way, the two words sound natural together, because we have a stress every three syllables. It's important to remember that the context of words affects how they are stressed.

Another example of stress being affected by context is the word "present." This word will be pronounced pre-SENT if it is a verb, but PRE-sent if it is a noun. So you always have to think about the meanings of words to determine how they should be read.

So how do you tell if a poem is in a particular meter? Well, to answer that, you need to know what the meters are. For example, anapestic tetrameter means that you have two syllables unstressed, followed by a stressed syllable, and that is repeated four times in a line of poetry. So, for example, if you wanted to know if Robert Frost's "The Road not Taken" is anapestic, you could write it out with the stress on every third syllable:

two roads DI-verged in A yel-low WOOD.

Okay, that sounds just plain silly. I'd say Frost's poem is not anapestic.

What about "The Night Before Christmas"?

'twas the NIGHT be-fore CHRIST-mas and ALL through the HOUSE.

Hey! That sounds nice! That's the way it's supposed to be read! So yes, that is an anapestic poem.

Then there's iambic poetry. A poem is iambic if you start with an unstressed syllable, and then alternate stressed and unstressed. So let's try Shakespeare's famous line "It is the star to every wandering bark." We'll try writing that out with alternating stress:

it IS the STAR to EV-ery WAN-der-ING bark.

Uh oh...that doesn't sound quite right. It worked well until we got to the word "wandering." Then things went screwy. But you know, lots of times, when we say wandering, we don't actually pronounce that middle syllable; we say "wandring." So let's try it that way:

it IS the STAR to EV-ery WAN-dring BARK.

Again, this starts out sounding right, but about the time we get to the word "A," it goes south on us. Who wants to emphasize the word "a" in a poem? Well, that's the thing; Robert Frost knew that if people read his poem naturally, without thinking about meter, the words "in" and "a" would both kind of get swallowed up - almost as though they were one syllable:

Two ROADS di-VERGED (in a) YEL-low WOOD,
and SOR-(ry i) COULD not TRAV-el BOTH
and BE one TRAV'ler, LONG i STOOD
and LOOKED down ONE as FAR (as i) COULD
To WHERE it BENT (in the) UN-der-GROWTH.

Okay, now stop yelling, and go read that stanza in your natural voice. Isn't it beautiful? That's poetry for you!

Related post: How does context affect stress of syllables?

Today's post is about a picture that has been mystifying and frustrating people. Frustrating because it seems so blatantly and completely wrong. Mystifying because people in the know just smile knowingly as though it's a joke.

Some jokes need to be explained, so here's the picture:

It seems quite clear, doesn't it? PEMDAS gives us our order of operations. We evaluated 85 + 65 first: 85 + 65 = 150.

So now we have 25 - 55 + 150, which should be evaluated in order from left to right: 25 - 55 = -30, and -30 + 150 = 120.

So how in the world did they get 5?

The answer is: they didn't get 5. They got 5!

You see, this is one of those horrible times when mathematics hijacks innocent punctuation marks and forces them into hard labor for nefarious, non-grammatical purposes.

The exclamation mark is used in mathematics not to epxress excitement or astonishment, but to indicate that we are calculating the factorial of a number.

What's a factorial? A factorial is what you get when you multiply all the integers between 1 and some number. For example, 6! = 6 x 5 x 4 x 3 x 2 x 1 = 720.

So before we declare this image bogus and invalid, we probably should check to find out what 5! equals.

5! = 5 x 4 x 3 x 2 x 1 = 120.

Oh! (And I'm using that exclamation mark to indicate astonishment) it really does equal 5!

And if I'm truly astonished, I might say that it equals 5!!

Except someone might get hoodwinked into thinking I meant 120!, which is about 6.8 x 10¹⁹⁸. That's not what I meant. I promise. I'm just that excited!

What is the solution to the following puzzle that's been going around facebook?

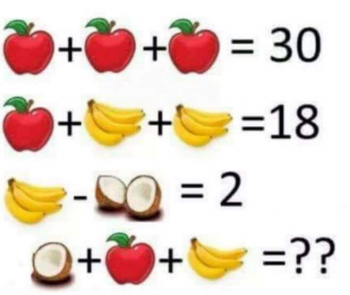
The answer is, on the surface, not terribly difficult to find:

3 apples = 30, so 1 apple = 10.

10 + 2 bananas = 18, so 2 bananas = 8 and 1 banana = 4

4 - 1 coconut = 2, so 1 coconut = 2

Therefore, 1 coconut + 1 apple + 1 banana = 2 + 10 + 4 = 16

HOWEVER...

Although this is the answer everyone seems to be giving, it's actually not correct. Notice that each bunch of bananas has four bananas (look closely!) except the one in the final line, which has 3 bananas. Also notice that the third line has one coconut, while the last line has only 1/2 of a coconut. 

This changes things!

3 apples = 30, so 1 apple = 10.

10 + 8 bananas = 18, so 8 bananas = 8 and 1 banana = 1

4 - 1 coconut = 2, so 1 coconut = 2

Therefore, 1/2 coconut + 1 apple + 3 bananas = 1 + 10 + 3 = 14

This is a really nice problem, since it gives you a good reminder to pay attention to details!

Click the image below to read Professor Puzzler's analysis of another puzzle:

Addendums

William from Phoenix asks, "Apples coconuts bananas: The editing to remove the fourth banana was incomplete. it left the end point in the picture on line four. Was that intentional to cause controversy with your answers?"

Honestly, William, I can't see the incomplete erasure you're talking about. I don't doubt you, but I'm not seeing it. But, since you asked, I'll take this opportunity to point out: I didn't create this problem; I just wrote up the solution for people who wanted to know. If I had to make a guess, I would say that the person who created it did not intentionally leave part of a banana; they probably were just inexperienced with photoshop, or were in a hurry when they created it! 

Colton from Florida had a question about the Algebra of this problem, which we answered here: Can X and Y have the same value?

Pany from UK points out that there is another way to interpret the problem, in which we regard each image as a symbolic variable, rather than as collections of real world objects. While I don't agree with him that this is the best way of looking at it, it is absolutely a valid way of viewing the problem, and it results in a very different problem, which is unsolvable, because we have more variables than equations. And speaking of which...

Anne from Maine shared with us a similar looking problem with a very different solution. Click the image below to read that post:

"Where does the apostrophe go in Presidents Day? Is it before the 's,' after the 's,' or nowhere?"

This is a fun question to look at for the month of February. In a couple weeks students across the country will be on vacation for a week, and their vacation will begin with the federal holiday called...

Presidents Day?
President's Day?
Presidents' Day?

Which is it? The surprising answer is: None of the above!

That's right - there is no federal holiday named any of those variations on "Presidents Day." The actual federal holiday is named "Washington's Birthday," with the apostrophe before the 's,' because we're only celebrating one Washington. If we were celebrating George Washington and George Washington Carver, we would call it "Washingtons' Birthdays" or something like that.

But if the holiday is officially known as "Washington's Birthday," why do we call it "Presidents Day"?

The answer to that stems from the fact that Lincoln's birthday is near Washington's birthday, and there was a push to make the holiday a celebration of both birthdays. And there was also a push to make it a celebration of all presidents.

Who made this push? Various states. You see, even though the holiday is officially called "Washington's Birthday" by the federal government, many states have implemented their own names for the holiday.

Which brings us back to the original question, with the qualification that now we're talking about state holidays. And the answer is: ALL THREE.

That's right; since each state gets to implement their own state holidays, and none of them agree, exactly, on how to implement it, the holiday gets named differently depending on how the state intends it to be celebrated.

For example, if you live in New Jersey (and a few other states), you celebrate the day without any apostrophes. Congratulations, New Jersians - you don't have to worry about where that apostrophe belongs!

If you live in Texas, you are celebrating multiple presidents, so you celebrate "Presidents' Day."

If you live in Maine, you are either celebrating a single president (presumably Washington) or you are celebrating the office of president, because you celebrate the singular "President's Day."

Some states choose not to use the word "President" at all, calling the holiday things like "Washington's Birthday" or "Lincoln's Birthday" or the somewhat convoluted title "Washington's and Lincoln's Birthday." 

Montana seems to prefer Lincoln over Washington, since they reverse it to "Lincoln's and Washington's Birthday"

Interestingly, a couple southern states eliminate Lincoln altogether from the holiday; Alabama replaces him with Thomas Jefferson, and Arkansas replaces him with civil rights activist Daisy Bates.

Did your state not get mentioned in this post? Head on over to Wikipedia and search for "Washington's Birthday" and you'll get a more detailed analysis.

And enjoy your holiday, whatever you might call it!
Professor Puzzler