We've had several questions recently about how to find terms of a geometric sequence, if you've been given specific information about the sequence, such as, what two of the terms are.

So let's consider a couple examples. For starters, let's say we have a sequence in which the second term is 4, and the fifth term is 27/2. How do we find the first term and the common ratio?

First, since the n^th term is ar^n-1, we know that ar = 4, and ar⁴ = 27/2. So what do we do with these two pieces of information? Well, we can take the second equation and divide it by the first one, to obtain r³ = 27/8, or r = 3/2.

Since we know that r = 3/2, we can plug that into our first equation, and get (3/2)a = 4, so a = 8/3.

Not too bad, right?

So let's try another one that works out to be just a little different.

If the second term is 24, and the fourth term is 6, find the first term and the common ratio.

We start out the same way:

ar = 24, and ar² = 6. Dividing these two equations gives r² = 1/4.

At this point, it's tempting to take the square root of both sides and say r = 1/2. (I see algebra students do this all too often!)

However, it's important to remember that 1/4 has TWO square roots: 1/2 and -1/2.

This means there are TWO possibilities for a. If r = 1/2, then a = 48, but if r = -1/2, then a = -48.

As a general rule of thumb, if you're given two terms of the same parity (both odd numbered terms, or both even numbered terms) you're going to have two possible solutions.

Thanks for asking, and good luck with your sequences!
Professor Puzzler

This site has an extensive reference unit on the topic of Codes and Secret Messages, and because of that, people often make the assumption that I want to help them decode their own personal secret messages. This is actually rarely the case. Actually, I think in decade plus that this site has been online, there's only been one instance where I helped someone decode a secret message. It was a Harry Potter code, and I turned it into one of the "Easter Egg" pages on the site (good luck finding it!).

I've even put a notice on the "Ask Professor Puzzler" contact page, letting people know that I'm not in the business of translating their secret messages for them. But the codes keep coming.

So we've added a new section to the community forum called "Codes and Secret Messages". This is a place where - if you are a member - you can post a code, and ask the community for help decoding it. Please note that in order to post a message in the forum, you must be a member, AND you must have played (and completed) at least five games on this site (that's our own version of a CAPTCHA - instead of asking you to read a convoluted, messy line of text, we ask you to solve puzzles; it's much more in keeping with the nature of the site!).

So if you've got a message, a code, or a riddle that needs decoding, head on over and ask for help!

Disclaimer: The following post is not a serious suggestion that we should revamp the way we teach students to learn addition. It's merely an interesting thought experiment.

It's true. You don't need all those addition facts. You spent hours and hours and hours memorizing 100 addition facts (0 through 9 plus 0 through 9). Okay, actually, you didn't learn 100 of them, because you learned that addition is commutative (5 + 7 is the same as 7 + 5, so you just need to memorize one of them).

But you don't need all those facts. You just need 25 of them (arguably, only 20*). Here's what you really need: 1. math facts for all whole numbers less than 5; and 2. and all the "fives" facts:

"Less Than Five" Table
0 + 0 = 0
0 + 1 = 1
0 + 2 = 2
0 + 3 = 3
0 + 4 = 4
1 + 1 = 2
1 + 2 = 3
1 + 3 = 4
1 + 4 = 5
2 + 2 = 4
2 + 3 = 5
2 + 4 = 6
3 + 3 = 6
3 + 4 = 7
4 + 4 = 8

"Fives" Table*
0 + 5 = 5
1 + 5 = 6
2 + 5 = 7
3 + 5 = 8
4 + 5 = 9
5 + 5 = 10
5 + 6 = 11
5 + 7 = 12
5 + 8 = 13
5 + 9 = 14

That's a total of 25 addition facts. And you can do all addition problems with just these, as long as you're willing to mentally split numbers that are bigger than 5.

Here's what I mean. Suppose you have to add 4 and 8, but you don't remember what 4 + 8 is. What do you do (besides counting on your fingers!)? You split the 8 into 5 and 3 (because, according to your "fives" table, 5 + 3 = 8). So now you have 4 + 8 = 4 + 5 + 3. Since two of those numbers are less than five, you know their sum: 4 + 3 is 7. Now use your "fives" table to get 7 + 5 = 12.

Let's try another. Add 7 and 9. Split one of those up using the "fives" table: 7 + 9 = (5 + 2) + 9. Since we have our fives memorized, we do 5 + 9 = 14. Now, since we know 4 + 2 = 6, 14 + 2 = 16.

We could have done the problem by splitting 9 instead of 7: 7 + 9 = 7 + (5 + 4). You know 7 + 5 =12, and since 2 + 4 = 6, 12 + 4 = 16.

The process is:

1. Split the larger number using your "fives" table.
2. If you now have two numbers less than five, use your "less than five" table, followed by your "fives" table
3. Otherwise, combine the number that's bigger than five with the five, using your "fives" table. This will result in a carry, and then you can use your "less than five" table.

* The "Fives" table is actually shorter than this. You only need to remember the pairings:

0 and 5
1 and 6
2 and 7
3 and 8
4 and 9

For example, consider the pairing 4 and 9. 5 + 4 = 9, and 5 + 9 = 4 (plus a carry).

This brings the total number of necessary facts to 20.

Or you could, you know, just bite the bullet and memorize all of them. :D

Kendrick asks, "What is the meaning of the phrase straining at a gnat?"

Good question! The phrase comes from the words of Jesus, as recorded in the Gospel of Matthew. In Matthew 23, Jesus launches into what could best be described as a tirade against the religious leaders of his day. He doesn't hold back in his indictment of them, and calls them names like "hypocrite," "family of snakes" (technically, he calls them a "brood of vipers," but that's the meaning), and "whitewashed sepulchers."

In verse 23, he says: "Woe unto you, scribes and Pharisees, hypocrites! for ye pay tithe of mint and anise and cummin, and have omitted the weightier matters of the law, judgment, mercy, and faith: these ought ye to have done, and not to leave the other undone."

What does he mean by this? He's saying that they've picked out the smallest and least commandments to focus on, and take pride in doing those, while completely ignoring the most important matters, like justice.

He follows this up in verse 24 with the phrase you asked about: "Ye blind guides, which strain at a gnat, and swallow a camel."

Jesus is indulging in a bit of hyperbole here. He's imagining someone who is about to take a drink of water from a cup, notices that there's a small bug in it, strains the bug out, and then drinks the water, never noticing that there was a camel floating in the cup.

Silly? Sure, but it gets the point across. Jesus' claim was that the religious leaders were focusing on the lesser matters, while completely ignoring the more important ones.

A similar idiom would be "penny-wise and pound-foolish." Someone who is penny-wise is someone who is very careful about how they spend small amounts of money. Someone who is pound-foolish is someone who throws about large amounts of money indiscriminately.

So someone who is both penny-wise and pound-foolish is straining at a gnat (focusing on small things) while swallowing a camel (ignoring larger things).

Would you like a modern day example of straining at a gnat and swallowing a camel?

As a teacher, if I gave a student a detention because he was slouching in his chair, but did nothing when he punched a classmate in the face, then I'm straining at gnats while swallowing camels.

By the way, if you have the time, you should take a few minutes to read Jesus' entire tirade against the religious leaders. Because we tend to think of Jesus as "meek and mild," this chapter can be quite astonishing to a lot of people: Matthew 23.

Krish asks, "In your base 11 Vortex Math, what brought you to begin with the number 2 rather than 1?"

For those who don't know what this question is in reference to, you'll want to visit our Vortex Based Mathematics page, where we explore (for a little bit of fun and enlightenment) what Vortex Based Math would have looked like if Marko Rodin was the proud owner of eleven fingers instead of just ten. It's a bit tongue-in-cheek, but it's a way of helping people understand the fundamental concept that Marko missed out on: bases.

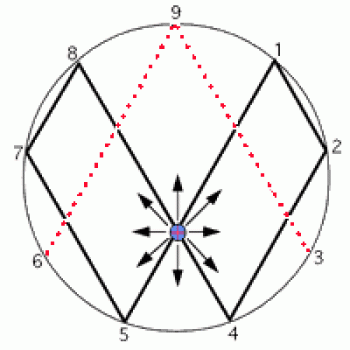
In Marko's base ten diagram (which he and his followers have been known to refer to as an equation, even though picture  and equation are not even remotely similar), Marko uses a doubling process to create a "loop" of numbers.

The numbers 1, 2, 4, 8, 7, and 5 each map to the next number in the sequence, with the number 5 mapping back to the number 1.

This produces an approximate infinity symbol, which, to Marko's way of thinking implies that this is going to result in an infinite supply of energy for everyone.

So my imaginary Seussian friend from Wunfishia, whose name is Marko-11 (because he has eleven fingers) did the whole process in base eleven. And his diagram looks like the one over on the right.

Notice that Marko-11 skipped over the number 1, and started his loop with the number 2. This is the source of Krish's question: "what brought you to begin with the number 2 rather than 1?"

The answer to that question might surprise you: I didn't start with the number 2; I started with the number 1! This was when I was doing the math for myself before I started writing up the page. 1 maps to 2, 2 to 4, and so forth. I was actually a little surprised when the mapping from 6 went back to 2 instead of to 1.

That was when I discovered "feeders" - numbers that aren't part of the loop, but feed into it. If you look at the picture below, you'll see that in base eleven, the vortex diagram has four feeders - four numbers that are not part of the loop, but feed into it.

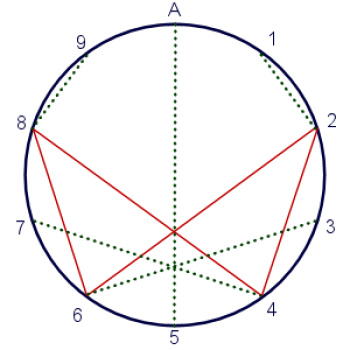
Once I understood that, I realized that it would be simpler to start with 2 when I was explaining VBM-11, and then show the "feeders" once I established the loop. The reason for doing that was purely pedagogical; I thought it would be easier for people to understand if I fully explained one concept before moving on to the next.

So let's wrap up with one more interesting question (which I have not yet explored):

In some bases, the loop starts with the number 1, in some bases it starts with the number 2, and in some cases it even starts with 3 or 4 (here's an example that starts with 4: Vortex-29). The question is: what is the pattern? Someday I may explore that question mathematically, but in the meantime, if you go to our Vortex-n-k simulator page, the website will do all the doubling and looping math for you, so you can quickly scroll through various vortex diagrams and see which loops start with 1, and which ones don't.

Have fun!
Professor Puzzler