I don't normally do follow-up posts on subjects I've already written up, because most of the time when I get e-mailed questions or comments about things I've written, I feel like they are best suited to a discussion in our community forum, rather than creating extra blog posts. However, this particular question, even though it is a follow-up to the Apples, Bananas, and Coconuts blog post, is worth analyzing in its own right, independent of the previous blog post.

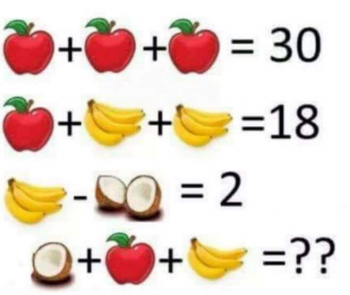
In the image shown here, the challenge was to find the value of an apple, three bananas, and half a coconut. There are multiple ways of assigning meaning to the images. For example, your basic banana "unit" could be 1 banana, or it could be 1 banana bunch (in which case, the last line contains 3/4 bunch!).

Similarly, your basic coconut unit could be a coconut, or a half-coconut. How you define these will affect how you work out the problem, but does not affect the solution.

One reader was concerned by the fact that you can end up with two variables having the same value: a half-coconut has the same value as a banana, and "this is not algebraically correct, as in algebra, X & Y cannot both be equal to one."

And this is the question we're exploring here: Can two variables have the same value in a problem?

The question-writer is not the only one who gets flustered by this possibility -- I have algebra students who get flummoxed every time I give them a problem in which both X and Y have the same value; they are convinced they must have done something wrong! In fact, just last week I gave my algebra students a system of three equations in three unknowns, in which the variables x, y, and z all were equal to one.

Really, there is no algebraic reason why two variables can't have the same value.

First, let me give you a graphical representation of an equation. Consider the following equation: y = 4 - x. If you graph it, it looks like this: 

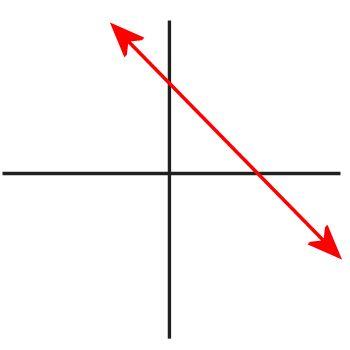
But what does that graph mean? It is simply a graphical representation of every ordered pair (x,y) that satisfies the equation. The red line is an infinite series of x and y values that make the equation true. But did you realize that there's a point in that graph for which x and y have the same value? It's true! It's the point x = 2, y = 2, because 2 = 4 - 2. If having two variables with the same value was illegal, then your algebra teacher would have taught you to graph the equation like this instead, leaving out the point (2,2):

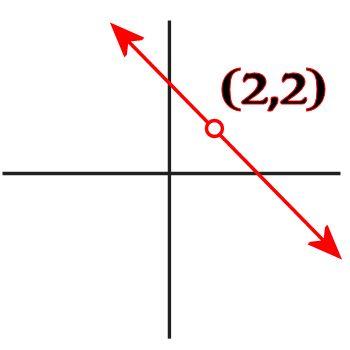
But your teacher didn't tell you to graph lines like this. Why? Because it's perfectly okay for two variables to have the same value!

There are practical implications that would result from supposing that x and y can't have the same value, because algebra was designed to have real-world application. Imagine an accident reconstruction expert is trying to figure out what happened when two vehicles collided. He sets up equations, assigning variables to all his unknowns, plugs in the values he does know, and then calculates the values of his uknowns.

Then, when he gets to the end of his calculations, he says, "Wait! This accident can't possibly have happened! Because the initial speed of the first car was 45 mph, and the initial speed of the second car was also 45 mph! We can't have the same value for two variables!"

No, of course he doesn't say that! In fact, if the speed limit was 45 mph, he'll just smile and say, "At least they were both going the speed limit!"

Or suppose you go shopping, and you pick up a bag of apples and a bag of pears. The bag of apples has 20 apples, and costs $4.00. The bag of pears has 10 pears, and costs $2.00. You think, "I wonder what is the cost of a single apple, and the cost of a single pear?" So you do set up two equations: 20a = 4 and 10p = 2, and to your horror, find that both apples and pears cost the same per fruit "That can't be right," you say, as you hurriedly put the fruit back on the shelf, "I had two variables, and they both came out to the same value!"

Of course not! You'll buy the apples and the oranges at the same unit price, and the universe won't explode! Because, you see, the real world doesn't really care about whether two quantities are equal or not. The values are what they are, and life goes on.

Someday I'm going to write a system of 26 equations in 26 unknowns, in which all 26 variables have the same value. My students' brains might explode, but nothing else will!

Historical note on this blog post: This question was originally asked and answered in 2005 - more than a decade ago! It became one of the most popular pages on the "Ask Doug" blog, and began circulating widely on the internet. As it went along, portions of it were modified, garbled, or even deleted, until eventually it came to the attention of those kind folks at Snopes, who wrote an article about this article, verifying the information within it. Imagine my surprise when one day my wife received her weekly Snopes e-newsletter, and at the top of the e-mail was my blog post!

The blog post has been moved to the "Ask Professor Puzzler" blog as part of our process of consolidation.

Question: I got an email from my * company, and it talked about logging in at their 'secure site', and it mentioned https and http. What is that?

Answer: HTTP stands for HyperText Transport Protocol, which is just a fancy way of saying it's a protocol (a language, in a manner of speaking) for information to be passed back and forth between web servers and clients. You really don't need to know what it all stands for; the important thing is the letter S which makes the difference between HTTP and HTTPS.

The S (big surprise) stands for "Secure". You probably didn't need me to tell you that, because you already knew it had something to do with security. If you visit a website or webpage, and look at the address in the web browser, it will likely begin with the following: http://. This means that the website is talking to your browser using the regular 'unsecure' language. In other words, it is possible for someone to "eavesdrop" on your computer's conversation with the website. If you fill out a form on the website, someone might see the information you send to that site.

This is why you never ever ever enter your credit card number in an http website!

 But if the web address begins with https://, that basically means your computer is talking to the website in a secure code that no one can eavesdrop on. You understand why this is so important, right? If a website ever asks you to enter your credit card information, you should automatically look to see if the web address begins with https://.

If it doesn't, there's no way you're going to enter sensitive information like a credit card number!

It should be pointed out that just because a website has that magic "S" in its address, that does not mean it is wise to do business with them; even scam artists can have https sites!  It simply means that no outsiders can eavesdrop on your conversation...doesn't mean you should be having the conversation in the first place.  Only do business with reputable firms, or firms you have thoroughly checked out!

Leap year! What is it good for? Absolutely nothing? Or does it actually serve a purpose?

Okay, let me explain how this question came about... 

Today our little girl turned one year old. She was born at 1:09 in the afternoon on February 11^th, 2015. I mentioned this to my Algebra students today, and then added that at about 7:09 this evening, she will have completed one entire revolution around the sun.

They looked at me like I had a third eye growing out of the middle of my forehead (okay, they often look at me that way...). "If she was born at 1:09 in the afternoon, isn't that when she's finished her first revolution around the sun?"

Nope! You see, a year is not exactly 365 days long. A year (the amount of time it takes for the earth to travel once around the sun) is actually a little bit longer than 365 days. It's right around 365.25 days. So our little girl finished her first trip around the sun a quarter of a day after her birth hour. Since a quarter of a day is 6 hours (²⁴/₄ = 6), and 7:09 is six hours after 1:09, it was this evening that she finished her first trip around the sun.

This led the class into a discussion of leap year, because that quarter of a day is the reason why leap years exist. If our calendar year is a quarter of a day shorter than a solar year (a solar year is the time it takes earth to travel once around the sun), then every four years, we'll end up with an extra day that needs to be stuffed into the calendar somewhere. So we decided to make that day be February 29^th. It was actually very good thinking - since February was by far the shortest month, putting that extra day in the calendar in February helps to even out the months a little*.

"Of course," I added, "It's not exactly that simple, because a solar year is not exactly 365.25 calendar days. It's just a little bit less than that. Which is why, every hundred years, we skip a leap year."

"WHAT?"

"Oh yes. If the year number is divisible by 100, we don't have a leap year."

"Really?"

"Sure. Unless, of course, the year is also divisible by 400. In that case, we do have leap year."

It was at this point that one of my students suggested that Leap Year might be good for absolutely nothing. Actually, what she said was, "I don't see why we need to do all this math. Why can't we just forget leap year?"

Ah. Good question. Let me try to explain it to you. Take a look at the picture below. In it you'll see the sun, and planet earth. Earth is following that almost-circular orbit around the sun, and I've marked the position of the earth with the time: the time of my little girl's birth.

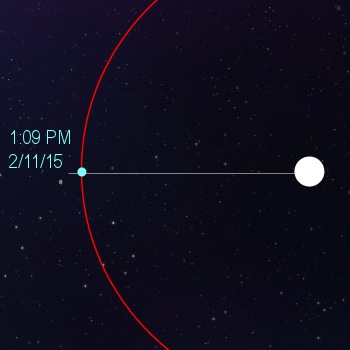
When the earth is in this position, we are essentially in the dead of winter.

Now, where will the earth be 365 days after this point in time? I'll show you. In the picture below I've marked 1:09 PM on Feb 11, 2016. That's the second line I've drawn. "That's it?" you might think. "Why that's hardly any difference at all!"

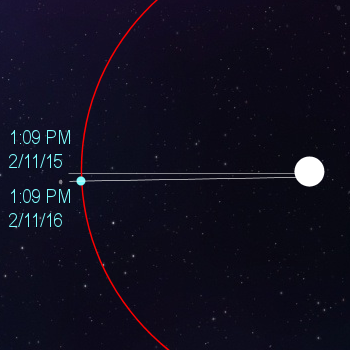
Sure, that's true. But that tiny little difference (about a quarter of a degree every year) will add up as the years pass.

Suppose we stop having leap years. And suppose that my little girl lives to be 120 years old (hey, who knows what scientific advances will happen in her lifetime?). When she's 120 years old, all those quarter days will have added up to an entire month. She'll be celebrating Christmas on December 25th, but the weather will be like Thanksgiving weather instead of Christmas weather, because the calendar year will have shifted an entire month from the solar year - and it's the solar year that determines our seasons, regardless of what we declare them to be on our calendar!

Can you imagine? She'll say to her great-grand kids, "I remember when we used to have blizzards on Christmas..." and they'll say, "That's silly, gram! We never have snow like that in December!"

And then, if we keep on like this, all those quarter-days will add up to 2 months, then 3. Eventually, our calendar year will be completely backwards from the solar year. Students will have June, July, and August off from school, and it will be snowing and bitter cold all through "summer" vacation. Then they'll be going to school all through the wonderfully warm and sunny beach weather of December, January, and February.

"Okay," my student said, "We can keep leap year."

I thought you might feel that way.

* Professor Puzzler's father, commonly known around here as "Mr. Physics," adds the following leap-year trivia:

"There is another reason whey they choose February for the extra day. Remember, under the Julian calendar the year started at March; February was the last month of the year. That is why September (7), October (8), November (9) and December (10) are numbered wrong.

"Another interesting bit of trivia. When Caesar Augustus decided that he needed a month named for him (August) he realized that to show himself equal to his Great Uncle Julius he needed to have 31 days in August so he stole a day from February leaving it with only 28 days."

I heard someone talking about the "Diameter of the Internet" recently. I understand finding the diameter of a circle; it's just the distance across its widest point. But what is the diameter of the internet, and how do you measure it?

Note: this item was originally posted on the "Ask Doug" blog* back in 2005. We've updated it and republished it with additional commentary at the bottom.

Have you ever played the game "Six Degrees Of Separation"? You start out with a person (often a movie star), and then see if you can relate them to another movie star in six or less connections. For example, how would you connect Julia Roberts to Sean Connery? Well, Julia Roberts starred with Richard Gere in "Pretty Woman", and Richard Gere starred with Sean Connery in "First Knight". That's two degrees right there.

The internet diameter is similar. How many degrees of separation are there between any two randomly selected web pages? How many clicks does it take to get from one web page to another? Researchers have done studies and calculations to try to determine the answer to this question, and the average "distance" in clicks between any two web pages is known as the diameter of the web. As of the turn of the millenium, the diameter of the internet was approximately 19 clicks.

And here we are in 2016, and you'd think we'd have updated statistics for you.

We don't.

We have some wrong statistics, though. Because, like everything else on the internet, people read what they want to read, and interpret things how they want to interpret them, with no regard for reality.

For example, in 2013, Smithsonian Magazine's website (yes, you read that right - I'm accusing Smithsonian of publishing bogus statistics - although, to be fair, they did partially retract their article) stated this information as though it was new, and reworded it to say that the maximum distance in clicks was 19. (Go back and read the original post; 19 was the average distance, not the maximum distance).

Others have made even more remarkable claims, such as "The diameter of the internet will never exceed 19."

But the reality is, nobody seems interested in continuing this line of study, and there doesn't appear to be any current statistical analysis on the diameter of the internet. So I guess we might as well keep saying the diameter is 19, even though that statistic is now about 16 years old!

There are some questions that would be fascinating to explore (if only I had more time!). Questions like:

• How do you deal with a website that is completely isolated (no inbound or outbound links)? Surely their distance to other websites isn't defined to be infinite? Because that would be problematic for averaging purposes! I suspect sites like that are dismissed from the equation.
• Did you realize that "distance" is not a "commutative" property? In the real world, if we say the distance from A to B is five miles, that means the distance from B to A is also five miles. But in the web, between any two points there are two distances - the number of clicks by outbound links from A to B, and the number of clicks by outbound links from B to A. These two numbers can be significantly different. To see why this is so, consider that there are thousands of websites around the world that link to The Problem Site. This gives a distance of one click. But The Problem Site doesn't link to most of those sites, which means the distance has to be more than one click. In fact, we should really think of it like distances between two cities when all the roads are one-way streets, so you have to take a different route from A to B than you would from B to A. So how do you calculate the distance? Do you take the smaller number? The larger one? Or the average?
• How are search engines included in the mix? Technically, Google links to virtually every website. But the pages that link to various sites are not static, because they are dependent on user input to display the links. On the other hand, if I search for "The Problem Site" on Google, and post the link here, I've now provided an indexable link for people to use when calculating the internet diameter. So have I changed my click distance to google by doing that?

Those are the questions that keep me up at night when I'm pondering 16-year-old statistics that no one else seems to care about any more! 

Professor Puzzler

* The "Ask Doug" blog was the precursor to the Ask Professor Puzzler blog. We are gradually moving the content from that blog to this location. Most items will be kept to their original publication dates, but occasionally, when we find an item of special interest, we'll re-post it with the current date, so our visitors will be more likely to find it!

A video has been floating around that talks about "fast thinking" and "slow thinking," and a simple three-question test that people who perform well on tend to do better on a lot of other tasks. Here are the three questions:

1. A baseball bat costs a dollar more than a baseball. Together they cost $1.10. What is the cost of the baseball?

2.  If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?

3.  In a lake, there is a patch of lily pads.Every day the patch doubles in size. If it takes 48 days for the patch to completely cover the lake, how long would it take to cover half the lake?

The video doesn't give answers or explain all the questions. Can you help?

I'll give it a go. But first, let me guess what the "fast thinking" (incorrect) answers are:

1.  The ball costs ten cents.

2.  It takes 100 minutes.

3.  It takes 24 days.

Were those the answers you came up with? If they were, don't feel bad - these are the "natural" answers. But let's look at the real answers.

Baseball Problem

If b is the cost of the baseball, then the cost of the baseball bat is b + 1.  This means that b + (b + 1) = $1.10. This leads us to 2b + 1 = 1.1, or 2b = .1. Dividing both sides by 2 gives us b = $0.05, or five cents. This is half of the instinctive response.

Widget Problem

You have 20 times as many machines, which means they can make 20 times as many widgets in five minutes. You know what that means, right? It takes 5 minutes!  All 100 of those machines are working simultaneously, and each group of 5 machines makes 5 widgets in that five minutes.  This is similar to the cat and mouse problem which can be found in our reference pages: Cat and Mouse Variation.

Lily Pad Problem

The correct answer to this is not half of 48; it's one less than 48. If the lake is half covered on one day, it'll be completely covered the next day. Therefore, it takes 47 days for the lake to be half covered.