Hi, I want know about 2-tier architecture and 3-tier architecture. Please explain me with some examples. Regards, Chandra

Chandra, The easiest way to explain this is, as you suggest, by an example. So I'll give you an example.

Let's suppose I'm going to write a piece of software that students at a school can use to find out what their current grade is in all their classes. I structure the program so that a database of grades resides on the server, and the application resides on the client (the computer the student is physically interacting with).

When the student wants to know his grades, he manipulates my program (by clicking buttons, menu options, etc). The program fires off a query to the database, and the database responds with all the student's grades. Now my application uses all this data to calculate the student's grade, and displays it for him.

This is an example of a 2-tier architecture. The two tiers are:

1. Data server: the database serves up data based on SQL queries submitted by the application. 
2. Client application: the application on the client computer consumes the data and presents it in a readable format to the student.

Now, this architecture is fine, if you've got a school with 50 students. But suppose the school has 10,000 students. Now we've got a problem. Why? Because every time a student queries the client application, the data server has to serve up large queries for the client application to manipulate. This is an enormous drain on network resources. So what do we do? We create a 3-tier architecture by inserting another program at the server level. We call this the server application. Now the client application no longer directly queries the database; it queries the server application, which in turn queries the data server. What is the advantage to this? Well, now when the student wants to know his final grade, the following happens:

1. The student asks the client application.
2. The client application asks the server application.
3. The server application queries the data server.
4. The data server serves up a recordset with all the student's grades.
5. The server application does all the calculations to determine the grade.
6. The server application serves up the final grade to the client application.
7. The client application displays the final grade for the student.

It's a much longer process on paper, but in reality it's much faster. Why? Notice step 6. Instead of serving up an entire recordset of grades, which has to be passed over a network, the server application is serving up a single number, which is a tiny amount of network traffic in comparison. There are other advantages to the 3-tier architecture (for example, a three tier architecture allows you to do load balancing, by having multiple servers that can function as the middle tier).

Incidentally, this website is a 3-tier application. The client application is your web browser. The server application is the php code which queries the database (the third tier) for the question-and-answer you requested. I hope that helps!

Phil's question is about the image below, and the blog post that goes with it (click the image to read the other blog post).

Professor Puzzler, in your answer to the "Genius" puzzle you showed a function that gave the right values for 8, 7, 6, and 5, but 3 wasn't in the domain. (I see how you did that, by the way - you multiplied the function by (x - 3), and then divided it by (x - 3) -- that gives you the same function, except with a hole in it!).

But my question is: can you come up with a function that matches all the data points given in the problem, but has a DIFFERENT value for x = 3? I'd like to be able to tell people that the answer is [some number besides 6]  and watch them squirm when I show them the function that gave that answer.

Hi Phil, I can absolutely give you a function that matches the data points given, and gives you an answer other than 6 when you plug in three!

Of course, you'll need to do a bit of memorizing, because it's kind of an ugly function. Are you ready?

g(x) = x⁴ - 26x³ + 252x² - 1067x + 1680

It's not pretty, is it? When you plug in 3, you get g(3) = 126, which is wonderful for what you want; it's quite startling that you get a result that's so big in comparison to the other data points. Your friends will think you're crazy for coming up with a number so big!

Are you wondering how I came up with this beast of a function? That actually wasn't too difficult. I was helped by the fact that I already had a function which matched the data points: f(x) = x² - x.

In order to create a new function that has all those same data points, I just need to find some function h(x) such that h(8) = 0, h(7) = 0, h(6) = 0, and h(5) = 0. If I have a function like that, I can just add f(x) + h(x), and I'll have my new function that keeps those same data points.

So what function h(x) meets the criteria of having zeroes at 8, 7, 6, and 5? EASY!

h(x) = (x - 8)(x - 7)(x - 6)(x - 5)

Multiply this thing out and you get:

h(x) = x⁴ - 26x³ + 251x² - 1066x + 1680

h(x) + f(x) = g(x) = x⁴ - 26x³ + 252x² - 1067x + 1680

Keep in mind that this is not the only such function; there are an infinite number of ways of generating your h(x), and different h functions will produce different values for g(3). For example, we could take our h(x) and multiply it by 1000, before adding f(x), and we'd still have a function that works. Or we could multiply it by some random polynomial like x⁷ + 17x³ - 11 (just make sure your polynomial doesn't have (x - 3) as a factor!). By doing this, we haven't changed the fact that the function has zeroes at 8, 7, 6, and 5. However, we've significantly changed the value of f(3)!

In fact, we could make g(3) equal anything we want to, just by manipulating our h(x) with a numerical multiplier.

Suppose we want to have g(3) = k. Then our function g(x) will be: 

g(x) = (^{(k - 6)}/₁₂₀)h(x) + f(x).

I'll leave it to the reader to figure out how I came up with that, and verify whether or not it works.

Now go annoy your friends, as only a math geek can!

The question of the day is: 

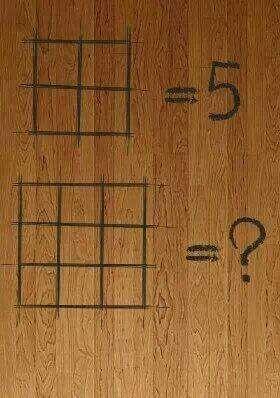
Can you solve it? If you said "yes," Then you are probably wrong. This is really not a "solvable" problem. It was created by someone who wanted to generate arguments and disagreements, because arguments translate into attention, likes, and shares.

You see, it's pretty much impossible to draw conclusions about a pattern when you only have one example from which to draw your conclusions. Depending on what pattern you notice, there are a multitude of "correct" answers.

I think the most common conclusion is: 5 is the number of squares in the image (four little ones and one big one). If this was your interpretation, then the answer is 14 (9 little squares, four medium squares, one large square).

However, there are other ways of interpreting the image. 5 is the number of line intersections involving interior line segments. In which case, the number for the second image is 12.

Another way of looking at it: 5 is the number of squares which border on the edge of the diagram. In which case, the answer to the second diagram is 13 instead of 14, because one of the squares (the central little square) doesn't border on the edge of the diagram.

But we don't have to stop there - as Brian Twitchell (District Math Coach, RSU #74) points out, we can create even more patterns:

• If we take one less than the number of horizontal unit segments, we end up with an answer of 11.
• If we take seven less than the sum of the number of horizontal and vertical unit segments, we get an answer of 17.
• Forget unit segments; consider line segments that span the length/height of the diagram. Now subtract one. This also matches the original diagram, and gives an answer of 7.

 So don't be too quick to assume you have "the" answer to a question!

If you enjoyed this post, you might also be interested in Professor Puzzler's analysis of this sneaky problem:

The image below has been showing up in various incarnations on the internet. Sometimes with an image of Albert Einstein, sometimes with an image of Sheldon from "Big Bang Theory."

I especially find this meme ridiculous when it's accompanied by a picture of Sheldon posing this as a problem for Penny, because anyone who knows Sheldon, and knows anything about math, know perfectly well that Sheldon would never, ever, ever pose a problem like this. Instead, he would, like good ol' Albert in the image below, give it an emphatic thumbs down.

What would Sheldon say the answer is?

He would say, "Three. The answer is three. Bazinga!"

Einstein probably wouldn't say "Bazinga," but he would agree. The answer is three.

"But," someone might protest to Sheldon, "That doesn't fit the pattern!"

"Oh," Sheldon would say, "You want a pattern? Okay. The answer is the square root of seventeen."

"No," you would say, "That's wrong."

"Exactly," Sheldon would say. "You wanted me to create a pattern. The first four equations are wrong, so I made another wrong equation to complete the pattern. Bazinga again!"

Einstein would probably answer differently. He would probably say, "Just because the first four equations are wrong doesn't mean I have to be wrong, too. The answer is three."

You see, in mathematics, the equals sign has a very specific meaning; it means that the two sides of the equation are equal. So I don't care if the person who made this meme got four equations wrong, the answer is still three.

What the problem writer probably meant to do was to use function notation:

f(8) = 56
f(7) = 42
f(6) = 30
f(5) = 20
f(3) = ?

Now we at least have valid mathematical notation. But is the problem solvable? Not really, no. Because there isn't just one function which satisfies the values above, and not all of them produce the same value for f(3).

For example, the function that the image creator probably wanted you to use was: f(x) = x² - x, which works for all the values given, and gives f(3) = 3² - 3 = 6. This is the answer most people are accepting as correct. However, consider the following as an alternative function:

f(x) = (x³ - 4x² + 3x)/(x - 3)

With this function, we get the correct values but we can't plug three into the function because it results in a divsion by zero!

So, even if we fix the notation, the real geniuses will tell you that it can't be solved.

Bazinga.

Addendums

• Phil wanted to know if I could find a function that matched all the data points in the pattern. but produced a different value for f(3). (Apparently he thought it was cheating to create a function that has no value for f(3)!). Anyway, the answer is, yes, I can do it, and here's the explanation of how: Creating Einstein's Meme Function.
• Toward the end here I'm being a bit tongue in cheek, pointing out that there isn't just one solution. For most of us, though, if we can find a pattern that matches four data points, we feel like we've come up with a satisfactory "solution."  It's a whole different matter if you're given only one data point and asked to find a pattern, which is what happens in the puzzle linked below. Be sure to read about the "squares" problem for more about that!

Click the image below for another question and answer!

Seventh grader Colton from Florida asks, "If triangles have the same area, are they similar? Or do triangles have to have the same perimeter to be the same? I think it's area. Thank you "

Hi Colton! 

Thanks for your question. I want to make sure we're talking about the same thing here. In one question you talk about triangles being "similar" and in the next you talk about them being "the same." These are two very different questions, that use very different concepts.

You see, triangles could be congruent (what you might have meant when you said "the same") or they can be similar.

So what is the difference?

Congruent means that two triangles are identically shaped. The have the same shape and the same size.  They have three pairs of sides that are the same length, and they have three pairs of angles that are the same measure. We call the pairs of parts "corresponding parts," and we say that in congruent triangles, "Corresponding parts of congruent triangles are congruent" (which gets shortened, often, to "CPCTC").

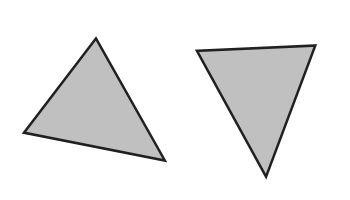
Another way of saying that: if you have two triangles that are congruent, you could pick one of them up and set it down on top of the other, and they would match perfectly. You might have to flip or rotate the one you picked up, but if you can't make it line up perfectly on the other triangle, they aren't congruent. In the image below, the triangles are congruent, because you could pick up the one on the right, rotate it about 45 degrees counter clockwise, and it would fit exactly on top of the triangle on the right.

As for your question: if two triangles have the same area, are they congruent? Not necessarily! I can create two triangles that take up the same amount of space, but have very different shapes. And the same is true of perimeter; just because two triangles have the same perimeter, that doesn't mean they're the same shape.

There are ways to tell if two triangles are congruent. For example, if you have two pairs of sides that are the same length, and the pair of angles between those sides is congruent, then it's guaranteed that the two triangles are congruent. Maybe in another blog post I'll explore all the different congruence theorems!

But now we need to consider similarity. Similarity is different from congruence. Two triangles can be similar without being congruent. Two triangles are similar if they have the same shape, but not necessarily the same size. What do I mean by "same shape?" Well, one way of explaining it is to say that all of their pairs of angles are congruent. 

Or, imagine that you have two similar triangles printed on transparencies. You might not be able to lay one on top of the other so that they match, but if you hung one of them on the wall, and used a projector to project the other one onto the wall, you could make them line up by getting the projector the right distance from the wall.

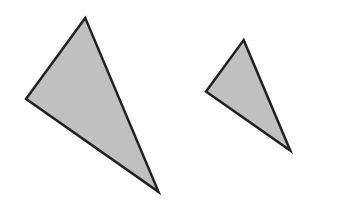
This picture is an example of two triangles that are similar. You can see the shape is the same; they both have two smallish angles, and one bigger angle. You couldn't lay one of them on top of the other and have them match perfectly, but if you expanded the smaller one, you could make it fit perfectly on the larger one. They are similar.

Okay, so now we come back to your question: if two triangles have the same area, or the same perimeter, are they similar? Not necessarily! You could have two triangles with the same perimeter (or the same area) that aren't the same shape at all. And if they're not the same shape, they're not similar!

So, in conclusion, neither the area nor the perimeter will help you determine if two triangles are similar, or determine if they are congruent!

That's a pretty long answer to a short question, but hopefully you learned some important concepts along the way.

Thanks for asking your question, Colton.

Sincerely,
Professor Puzzler