Vera from Michigan asks, "What is a star operation?"

First, let's talk for a second about operations in general. Operations are things that we can do to one or more expressions in order to create a new value from them. I say "one or more," because it's possible to have an operation that works on a single expression; we call that a unary operator. Most operations that you're familiar with take two expressions and combine them to make a new expression. We call these binary operators. In this blog post we'll talk about binary operators, and maybe someday I'll come back and do a blog post about unary operators.

What are some examples of binary operators? Multiplication is a good example:

3 x 5 = 15

In this example, we took two expressions (3 and 5) and we used the multiplication operator (x, or •) to combine them to create a new value:15. Now, you know that 3 x 5 = 15 because you memorized it at some point, but it wasn't just arbitrary memorization that got our result; the operation has a rule that gives you the result. The rule can be expressed in a few ways - here are just a couple:

• count to 3, five times. How many numbers did you count?
• create a rectangle that's 3 units wide and 5 units long. What is the area of the box in square units?

Every operation has a rule, or pattern, that we use to combine the two expressions into a single expression.

What are some other operators you're familiar with? Addition (+), subtraction (-), division (/).

But what is a star operation? Well, math teachers get bored, sometimes, with so few operations to confuse their students with, so they feel like inventing their own operations, complete with their own rules and their own symbols. Since the asterisk isn't used as an operation symbol (except in computer programming), we often use the asterisk as our operation symbol. Since the asterisk looks like a star, we dubbed it a "star operation." Let's look at an example:

Example One
We'll define our rule as follows a * b = a² + b².

This means that if we see something like 3 * 5, we'll plug the 3 in place of the a, and 5 in place of the b:

3 * 5 = 3² + 5² = 9 + 25 = 34.

Example Two
Rule: a * b = a(b - 1)

Find the value of 4 * 7.

In this case, we'll plug the 4 into our rule in place of a, and the 7 in place of the b:

4 * 7 = 4(7 - 1) = 4(6) =24.

By the way, it's interesting to note that our first example is commutative, which means that a * b = b * a, but the second rule is not. If we calculate 7 * 4 instead of 4 * 7, we don't get the same result:

7 * 4 = 7(4 - 1) = 7(3) = 21.

We don't have to use the asterisk symbol for our operation, by the way. We can pick any other unused symbol we want. It's not unusual to see a delta symbol (the Greek letter delta is a triangle with one vertex at the top) or an inverted delta symbol (pointing down instead of up), or a square, or a diamond, etc. We still often refer to them as star operations, even if they don't use the asterisk symbol.

Example Three
Rule: a ♦ b = (a + b)/2

Find the value of (2 ♦ 4) ♦ 6.

Notice that in this problem, we have parentheses, and our standard order of operations applies here - we have to evaluate the part in parentheses first:

2 ♦ 4 = (2 + 4)/2 = 6/2 = 3.

Now we evaluate 3 ♦ 6:

3 ♦ 6 = (3 + 6)/2 = 9/2 = 4.5.

As a side note, we observe that this operation is not associative; if we shift the parentheses, we get a different result: 2 ♦ (4 ♦ 6) = 3.5.

In closing, it can be fun to try to guess the rule for a star operation, given a table of values. Take a look at this example:

5 ¤ 3 = 16
7 ¤ 4 = 33
8 ¤ 6 = 28
8 ¤ 2 = 60

What do you think the rule could be? There could be more than one possible answer, and I'll leave it to you to figure it out. I'll give you one more equation to test your rule against:

1 ¤ 7 = -48

In my math classroom there hangs on the wall a poster I made, which looks something like this:

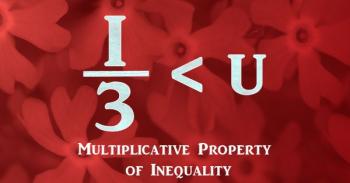
It usually takes quite awhile for my students to figure out the significance of the image. For one thing, they start out not knowing anything about the multiplicative property of inequality. When they ask me about it, I assure them that they'll learn over the course of the year a variety of properties of multiplication, and then they'll understand the poster.

What is the multiplicative property of inequality? The multiplicative property of inequality says that if you have an inequality, and you multiply both sides of the inequality by the same positive quantity, you will have an equivalent inequality. If you mutliply both sides by the same negative quanity, and change the direction of the inequality symbol, you still have an equivalent inequality.

Once my students understand this property, they look at the poster again, and since they all hate fractions, it doesn't take them long to decide they want to multiply both sides of the inequality by 3. This is a positive quantity, so they don't have to reverse the inequality sign. The result the obtain is:

I <3 U, which is an online shorthand for I love you (I - HEART - YOU).

Oh, those crazy, romantic, mathematicians!

I am Ben and I am in forth grade. I would like to know what a trojan horse is.

Well Ben, I notice that you said "a trojan horse," rather than "the trojan horse." That does make a difference in the explanation. First I'll review (in case you didn't know) what the trojan horse was, then we'll talk about how that phrase is used today in the world of computers.

Did you ever learn about the Trojan War? The Trojans were citizens of the city of Troy. The story of their war with the Greeks is recounted in Homer's Iliad, and other Greek literature. According to the story, the Trojans defended their city against the Greeks, but they finally lost when their enemies built an enormous wooden horse and hid a group of soldiers inside it. The Trojans thought it was a peace offering, so they brought it into the city and had a big party.

Then, in the middle of the night, while everyone was asleep, the soldiers climbed out of the horse and opened the city gates, letting in the Greek army. The Trojans were defeated because they were so gullible.

That's the trojan horse. But today we use that phrase to mean something similar, but different.

In computer terms, a Trojan Horse is a computer virus that is designed to fool people, just like the Trojans were fooled. It may be a program that is supposed to do something helpful, but really is also doing some unhelpful things.

Maybe you get an email that says "The attached file is an update from Microsoft. Open it to update your computer." Only, it's not really an update from Microsoft - it's a program that deletes all the files on your computer. But you believe the message, so you open the file. Now you're just like the Trojans. You thought you had something nice, but it turns out to be very nasty instead.That's a Trojan Horse.

Or you might be looking for a piece of software to do a particular job. Maybe you want some photo editing software, or screen capture software, or video conversion software. So you go looking online, and you find a free version of the software. You get excited about not having to pay anything, and you download it. But you don't realize that the software is actually spying on you, or damaging your computer in some way.

And by the way, that should be a good reminder to you of how cautious you should be when you download files from the internet, and when you open files attached to e-mails. Don't be like the Trojans - always be suspicious!

[Note: if you came to this post by way of DailyMail.co.uk, you should note that this article is based on a slightly different problem than the one they're talking about (look at the operations in the last line). Nevertheless, their proposed solution is still wrong (both for their problem and this one). Also, be sure to read our blog post about "Hard vs. Unsolvable!" Finally, if you're thinking about writing to us about this problem, please read the update at the bottom of this article.]

I should have known that after our write-up of the Apples, Bananas, and Coconuts problem went viral, we'd get asked to evaluate similar problems. Here's the latest one, and I wouldn't bother writing it up, except it has a fundamental difference from the banana problem. And people are taking the wrong lessons from the banana problem, and are still getting it wrong.

The correct answer to this question is, "No, I cannot solve this." There really is no other answer. If you came up with a numerical value, you were wrong (sorry!). Let me explain.

People who saw our write-up of the banana problem were quick to note that this problem has two similarities to that one: instead of two yellow flowers (as there are in the third line), there is only one in the last line, and instead of five petals (which it has in the second and third lines) the blue flower has only four petals in the last line.

The obvious (and erroneous) lesson to take here is that we're going to count petals instead of flowers. This leads people to the result of 25. So why is this wrong? Because the equations are not petal images; they are images of entire flowers.  We can calculate the value of a red flower, we can calculate the value of a yellow flower, and we can calculate the value of a blue flower with five petals, but we do not have any information with which to calculate the value of a blue flower with four petals. Unless we make the assumption* that the entire value of a flower lies in its petals. Ask a florist if he would sell a flower for the same price if the leaves and stem had been removed. I think you know what he'll say. 

Or we could make the assumption* that a flower is valued at the sum of its petals, stem, and leaves and also assume* that all petals, stems and leaves have the same value from flower to flower. In which case we could set up a system of three equations in 3 unknowns, with P representing the value of a petal, S representing the value of a stem, and L representing the value of a leaf:

36P + 3S + 3L = 60
22P + 3S + 3L  = 30
21P - 1S  - 3L = 3

And we need to find the value of 24P + 3S + 4L

If we subtract the second equation from the first, we get 14P = 30, or P = 15/7 (yuck).

You know what? I'm not going to follow through with this any further, because it's not a pretty system of equations, plus it's not inherently obvious that we should interpret the problem this way. So I think it's just a waste of my time.

* You will note that methods of attempting this problem will require us to make assumptions about the value of a stem, and the value of a leaf. And, furthermore, it requires us to make the assumption that each flower is worth the sum of its parts. Thus, the problem is unsolvable.

So I'm going to stick with my original answer: unlike the banana problem, this one is unsolvable.

So what is the big difference between the two problems? The difference is that in the bananas problem, each image was a representation of a number of fruits, so removing a fruit simply converts the image to another known quantity without fundamentally changing the nature of the objects represented, while in this problem the images are representations of entire flowers, so removing a petal doesn't convert it into a new known quantity; it fundamentally changes the nature of the object into something we don't know the value of.

That probably wasn't the answer the problem creator was looking for, but I don't really care - that's my answer, and I'm gonna stick to it!

Read more: Hard vs. Unsolvable!

Update June 17, 2016

This morning I received the following interesting email from Allan in Newcastle, Australia:

POLLEN PANDEMONIUM Why has nobody seen that the two yellow flowers are a multiplication (there is no + sign as there is in line 1), so that means one yellow flower is worth 1.4142.... (the sq.root of 2). The answer must therefore include .4142. I know you reject the following but . . .as the number of petals only matters for a blue flower, the answer is 25.4142.

Hi Allan! This is a fun way of looking at the problem. I don't think it's a correct way of looking at it, but it's still fun. I'll explain first why I don't think it's the correct way to look at it, but then, if you don't mind, I'll play a little game of "What if this WAS the correct way to look at it?"

Representing mathematical problems in a pictorial format is not a completely out-of-the-blue idea that the person who created this problem came up with. Math text books (especially at the younger grade levels) often use a pictorial format to illustrate math concepts. For example, in a lesson on place value, the number 27 might be represented by a picture of two rods (each representing 10), plus 7 squares (each representing one). In this case, the two rods represent exactly what they look like: two tens, not ten squared.

Similarly, if a textbook showed a picture of five dimes, a plus sign, and three more dimes, you should interpret that as a total of 8 dimes, not as 10⁵ + 10³.

So, even though I've never seen a rigorous definition of how we do pictorial mathematics, there's at least a "standard," and that standard suggests that a picture of two flowers really does represent two flowers, and not "flower squared."

Having said that, I've left a little loophole here; since I've never seen a rigorous definition, can we have some fun and see what happens if we choose to define it the way you did?

You said, in your e-mail, "the number of petals only matters for a blue flower," which is not strictly true. You see, one of the really important things we have to agree on in mathematics is that we be consistent in meaning, throughout a problem. Thus, if we need to deal at the "petal" level for blue flowers, in order to be consistent in notation, we need to deal at the "petal" level for all the flowers.

So the first equation is not 3r = 60, where r represents the value of a red flower. It's 3(12p) = 60, where p represents the value of a single red petal.

Except...if we agree to use your idea of using multiplication when no operation is presented, we now have to apply that at the petal level across the entire puzzle.

So it's not 3(12p) = 60; it's 3p¹² = 60, because we have to multiply together all those petals!

So if 3p¹² = 60,
p¹² = 20

Which means p is actually the twelfth root of 20, which is about 1.284!

And then, of course, you need to follow the logic through on the other equations as well. :) I'm not going to do that; I'll leave it for readers to play around with the problem and see what answer they get. Thanks for your e-mail, Allan; this was a fun way to look at the problem.

Update June 21, 2016

When this post went viral, we started getting a large number of e-mails from helpful people who wanted to make sure we knew how to do the problem. This was exceedingly bizarre, since the article is pretty clear that it's not that we don't know how to solve the problem, but rather that there is not enough information to solve the problem without making unwarranted assumptions and therefore it cannot be solved. With the exception of the message from Allan in Newcastle (see June 17 update), each of these e-mails has done nothing but make one of the assumptions which was already addressed in this post. It makes it very evident that people are responding to this article without reading it. For this reason, we're no longer replying to emails about this post; Professor Puzzler is getting tired of simply redirecting people back to the article they should have read in the first place! Click here to read more about ambiguous math problems.

This will Mess With Your Head. 3 MEN GO INTO A MOTEL. THE MAN BEHIND THE DESK SAID THE ROOM IS $30, SO EACH MAN PAID $10 AND WENT TO THE ROOM. A WHILE LATER THE MAN BEHIND THE DESK REALIZED THE ROOM WAS ONLY $25, SO HE SENT THE BELLBOY TO THE 3 GUYS' ROOM WITH $5. ON THE WAY, THE BELLBOY COULDN'T FIGURE OUT HOW TO SPLIT $5 EVENLY BETWEEN 3, SO HE GAVE EACH MAN A $1 AND KEPT THE OTHER $2 FOR HIMSELF. THIS MEANT THAT THE 3 MEN EACH PAID $9 FOR THE ROOM, WHICH IS A TOTAL OF $27, ADD THE $2 THAT THE BELLBOY KEPT = $29. WHERE IS THE OTHER DOLLAR? SEND THIS TO 5 PEOPLE AND THE ANSWER WILL APPEAR ON YOUR SCREEN.

First of all, let's clear up a misconception here. It doesn't matter how many people you forward this email to - the answer will never appear on your screen, unless someone decides to take pity on you and reply to your email.

Now, regarding the question of the three men and the bellboy, if this one stumps you, don't feel bad. I remember as a child puzzling over this one for a long time before I finally saw through the "trick". Believe it or not, the answer is exceedingly simple, and you don't need any advanced mathematics to figure it out.

What you've got to ask yourself is: If the men paid 27, and the boy took 2 from that, why in the world are you adding those two numbers instead of subtracting them? 27 - 2 = 25, which is the total amount paid. 27 + 2 is completely meaningless addition problem.

The thing that fools you into thinking it's a meaningful problem is the fact that the answer is close to 30, so you think it should add up to that. But there's no reason for that addition to add up to anything meaningful, because addition is not a meaningful thing to do with those two numbers in the context of the problem.

Also, the fact that there's an additional exchange (involving the man behind the desk) confuses the issue, and helps to distract you from the fact that the bellboy is really taking money from the guests.

Let me put it this way. If I gave you twenty seven apples, and someone took two away from you, would you then have 29? Of COURSE NOT! But that's exactly what the problem writer is trying to get you believe!

So when someone asks you "Why doesn't this add to 30?" just give them a puzzled look and say, "Why do you think it should?"

Added note: If you would like to see a similar problem click here: Guy Buying a Car.