A visitor from Nigeria asks, "What is the different between aceleretion and velocity?"

Acceleration and velocity are two quantities that we deal with in the field of Physics. They are related, but quite different concepts. 

Let's start by talking about something acceleration and and velocity have in common. They are both vectors. Back when I was in school, students never heard of vectors until they hit high school Physics class, but nowadays, most kids learn what a vector is much earlier than that. And they don't learn it at school. They learn it while watching the movie "Despicable Me."

The character Vector announces to Gru that his name is vector because, "I commit crimes with both direction and magnitude."

A vector contains two pieces of information - a size (magnitude) and a direction. Velocity and acceleration are both vectors.

Another way in which velocity and acceleration are similar: they both relate to the motion of an object.

Velocity is a way of defining the motion of an object. It can be described as a speed and direction of motion. For example, a car is traveling at 60 mph East. 60 mph is the magnitude, and east is the direction. I'm in an elevator that is going down to the first floor at a speed of 5 m/s. 5 m/s is the magnitude, down is the direction.

So what is acceleration? Acceleration is the rate at which the velocity is changing. It is also a vector, so it also has a magnitude and a direction. For example, In the elevator example above, if the elevator had an acceleration of 1 m/s²up, that would mean that every second, the speed of the object is decreasing by 1 m/s. So after one second, the elevator would be traveling at 4 m/s. After two seconds, it would be traveling at 3 m/s. And after five seconds, it would be standing still.

On the other hand, if the elevator had an acceleration of 1 m/s² down, the elevator would be speeding up.

If the cable on the elevator broke, it would have a downward acceleration of 9.8 m/s². As you might imagine, that would be downright terrifying. After one second, the elevator would have a velocity of 14.8 m/s down. After two seconds, 24.6 m/s down, which is about 55 mph down. Obviously, there's a good reason to be concerned if the cable breaks!

If the elevator had an acceleration of 1 m/s² west, that would mean that as the elevator is dropping, it's also picking up speed in a horizontal direction, which - I suppose - means it's crashing through the side of the elevator shaft!

Any time the velocity is changing, you have an acceleration. If the velocity is not changing, the acceleration is zero.

When I'm teaching acceleration to my physics class, I always ask them how many accelerators their car has. They usually respond by saying, "The gas pedal." I tell them that's not the only one. They ponder for awhile, and then realize that the brake is also an accelerator; it gives an acceleration in the opposite direction of the motion. I tell them they're still not done, and remind them that velocity is a vector, which includes a direction, and that acceleration is the rate of change in velocity. Eventually, someone realizes that the steering wheel is also an accelerator, because it changes the direction of the car.

Bianca, an 11th grader from Canada asks, "Hello, I need help in math, how can I prove that the cosine of 36 is equal to the number of gold divided by 2."

That's a great question, Bianca. For anyone who doesn't know, the "number of gold" or "the golden ratio" is the number (1 + SQR(5))/2, which is approximately 1.6180339887. This number is interesting largely because the Greeks were fascinated by it, and because certain sequences which appear in nature sort of "zero in" on this number.

So how do we prove that the cosine of 36 degrees is this magical number? Well, we'll start by drawing a picture of an isosceles triangle which has angles 36-72-72.

Let's add a line segment to this triangle; let's add an angle bisector from angle B to the opposite side.

This produces some interesting similarities and congruences. For starters, measure of angle DBC is half of the measure of angle ABC, or 36º. Since the measure of angle DCB is 72º, we have triangle ABC similar to triangle BDC, and BC = BD (because the triangle is isosceles).

We can use some similar reasoning on triangle ABD to conclude that it is also an isosceles triangle, with BD = DA.

Putting all of this together leads to BC = BD = DA.

Now, since triangle ABD is similar to triangle BCD, we can conclude that

AC / BC = BC / CD

BC² = (AC)(CD)

Now we can do a substitution, by noting that AC = AD + DC which equals BC + DC.

BC² = (BC + DC)(DC)

BC² = (BC)(DC) + DC².

At this point, I'd like to do two things to this equation. First, I'd like to divide both sides by DC², and then I'd like to do a substitution: x = BC/DC. This results in the following equation:

x² - x - 1 = 0.

This can be solved using the quadratic formula: x = (1 + SQR(5))/2, or the golden ratio!

But how do we get here from to the trig function you want? Well, for starters, since the larger triangle is similar to the smaller one, we also have AB/BC = the golden ratio.

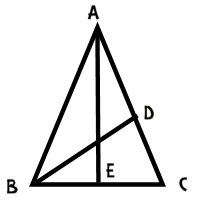
Now if we draw a perpendicular down the middle of the diagram, we've got AB/BE = 1/2 of AB/BC, or half of the golden ratio. This means that BE/AB is 1/2 of the golden ratio. But BE/AB is the cosine of 72 degrees, since AEB is a right triangle.

Thus, cos(72º) = 2/x, where x is the golden ratio.

From here we can use a half angle identity:

cos(36º) = SQR((1 + cos(72º))/2)

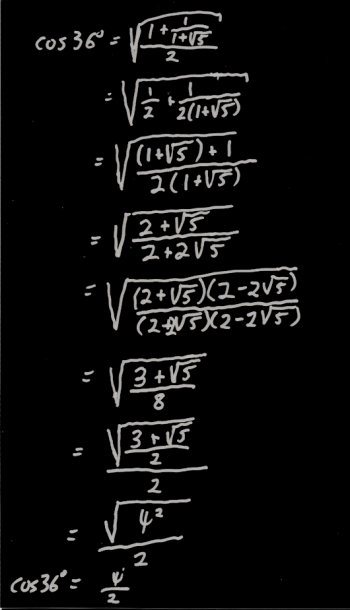
Now if you think that looks ugly, you're right. If you punch it into your calculator, you'll find that it evaluates to 0.809016994, which is half of the golden ratio. However, it would be nice to have an algebraic proof, right?

I worked through the algebra, but typing it all out on the blog would be UGLY, so I'm just going to post an image of the work I did on paper.

To view a larger version of this image, just click on it.

When I got to the end of the algebra, I had a radical within a radical, which is an ugly looking beast, but I happened to remember that (3 + SQR(5))/2 is the square of the golden ratio, which made the whole thing simplify quickly.

Is there an easier way to arrive at the cos(36º)? I'm sure there is. This was just the first one that came to mind. There might be other ways to do this using the law of cosines, or the law of sines, and I know you can do it with an entirely non-geometric proof (using various trig identities) but this one does the job. If you find a simpler proof, let me know!

Red, from Syria, asks, "How can I become better in knowing the differences between stressed and unstressed syllables beside practice ? Is there a secret I could use to seperate between stressed and unstressed syllables ? Thank you"

Hi Red, this is a tricky question, because the answer is different for every language. I'm going to hope that, since you're not from an English-speaking country, and you're writing to someone who answers questions in English, you want an answer about the English language. English is a very unpredictable language. Some languages, like Spanish, have very hard-and-fast rules for defining which syllable receives the stress (accent). English...not so much. But there are still some guidelines that will help you out. I'll cover a few here to get you started.

1. In general, we consider every English word to have one accented syllable. However, if it's a lengthy word, we might have syllables with a "secondary" stress. For example, we might say that the word "dodecahedron" has its stress on the syllable "dec" and a secondary stress on "hed." Notice that the pattern of stressed and unstressed syllables is an alternating pattern: do-DEC-a-HED-ron. This alternating pattern is quite common.
2. If a word has either a prefix or a suffix, it's unlikely that the accent falls on the either the prefix or suffix. For example, in the word "unlikely," "un" is a prefix and "ly" is a suffix, and both are unaccented. This leaves us with the inevitable conclusion that "like" is the accented syllable. Lest you think that's a guaranteed rule, just scan through this paragraph, and you'll find a counter-example: "prefix" is pronounced "PRE-fix," not "pre-FIX."
3. When in doubt, find the first syllable that isn't a prefix, and give that one the accent. That's also not a hard-and-fast rule, for sure, but it'll be correct more often than it's not. Consider the word "unpredictable" in the first paragraph of my response. "Un" and "pre" are prefixes, so we put the stress on "dict": "un-pre-DICT-able."
4. Some words have different pronunciations depending on the way the word is used. For example, the word "refund" can mean "an amount of money returned" or "to return some money." The first one (a noun) is "RE-fund" and the second (a verb) is "re-FUND." When faced with this sort of word, the safest guess is to assume that the noun has the first syllable stressed (even if, as is the case here, the first syllable is a prefix), and the verb has the next syllable stressed.
5. There are a few other rules you'll figure out as you go along, and the more you hear English spoken, the more you'll intuitively grasp them. For example, if you run into a word that ends with "ation," it's very likely that the penultimate syllable will have either the stress or the secondary stress, which will help you work out how to pronounce the word. Examples: pro-NUN-ci-A-tion, in-TER-pret-A-tion, etc.

Hopefully this will be helpful to you in learning better pronunciation. Of course, there is no substitute for spending time talking with native speakers and picking up their speech patterns! Thanks for your question, Red.

Gloria asked, "Does the popular vote not count if it's a landslide with the electoral college? How does that work?"

Gloria is asking about the presidential elections. We often talk about how much a candidate is "up" in the polls, and that's a measure of the popular vote. For example, as I write this, Secretary Clinton is, according to most polls, up by 5 to 10 percentage points. This means that 5% to 10% more voters are likely to vote for Secretary Clinton than vote for Mr. Trump.  

The definition of "landslide" is pretty nebulous; one source said that if one candidate earns 60%, that's considered a landslide. Of course, with the relative unpopularity of the current candidates, that's certainly not likely. However, with Clinton leading significantly over Trump at this point, many are referring to this as a possible landslide.

But even if that's true, does it guarantee a win for Secretary Clinton? No, it does not. Because it is not the popular vote that determines the result of the election. It's the electoral college. Every state is assigned a certain number of delegates who will cast an "electoral vote" on behalf of the people in their state. For example, California, because it is such a populous state, has 55 electoral votes, but Wyoming, because it has a much lower population, only gets 3 electoral votes.

So what does the popular vote decide? It decides who each state's electors must cast their vote for. In other words, if Secretary Clinton wins California, then all 55 Californian electors cast their ballot for her. If Mr. Trump wins Wyoming, then Wyoming's 3 electors vote for him.

It's an all-or-nothing deal in all but two of the states. Maine and Nebraska have rules that allow the electors to have a split between the candidates.

So, doesn't that mean that a landslide in the popular vote would result in a landslide in the electoral college? Not necessarily. To see why, let's break it down into a simple example. Let's pretend that the United States of America consists of only two states. Semi-random selection off a map: Michigan, and its neighbor, Ohio.

Ohio has a slightly larger population than Michigan, and therefore a slightly larger number of electoral college delegates. Ohio has 18, and Michigan has 16. We'll use 2012 statistics and say that 4.9 million people in Michigan will vote in the upcoming election, and 5.6 million Ohioans will vote.

Now, to make our example clear, we're going to depart from what's likely to happen and imagine an extreme scenario for these two states deciding the election. Let's say that Michigan votes overwhelmingly for Secretary Clinton:

Michigan votes for Clinton: 4.0 million
Michigan votes for Trump: 0.7 million
Michigan 3rd party votes: 0.2 million

Let's further suppose that Mr. Trump wins Ohio, but it's a much closer race than Michigan:

Ohio votes for Clinton: 2.7 million
Ohio votes for Trump: 2.8 million
Ohio 3rd party votes: 0.1 million

Who wins this election? Well, Secretary Clinton gets Michigan's 16 electoral votes, because she won the popular vote there, and Mr. Trump gets Ohio's 18 electoral votes, which means Trump wins the election.

But who won the popular vote? Was it a landslide? Let's find out:

Total votes cast: 10.5 million

Total votes for Clinton: 6.7 million, or 63.8%
Total votes for Trump: 3.5 million, or 33.3%
Total 3rd party votes: 0.3 million, or 2.85%

Is this a landslide? I think any reasonable definition of landslide would agree that in this extreme scenario, Secretary Clinton's win in the popular vote was a landslide. But even so, Mr. Trump wins the electoral college vote, 18 to 16, and becomes the next president.

So what happened? What happened is that in the state that supported Clinton, she trounced Trump, but in the state where Trump won, it was a much closer battle. Since it's an all-or-nothing battle in both states, how much she won by is irrelevant to which direction the electors cast their vote.

Now add 48 more states into the mix, and imagine this sort of scenario playing itself out over and over again. Some states are close, some are a blowout, but the electoral votes are (with the Maine/Nebraska exceptions) assigned all-or-nothing regardless of how big the margin was.

Chris, from Maine, points out that this is not just a theoretical exercise: " A president has lost the popular vote but won the electoral college four times, with the most recent being only 16 years ago!"

Finally we get to the issue that a candidate is required to get a majority of the electoral votes (270). What happens if no one hits that magic number is a question for another day.

Fourth grader Alice asks, "How many diagonals are in decagon?"

Great question, Alice. But instead of giving you an answer to that question, I'm going to show you how you can figure it out for yourself. And not only that, I'll show you how you can figure out the answer for any polygon, even if it has 20, or 50, or 2000 sides!

Ready? Let's start with a simple example. We'll go with a polygon that has 8 sides (which is called an octagon), like this:

Now, this polygon, because it has eight sides, also has eight vertices. It seems a bit overwhelming to try to figure out all the diagonals, so let's just focus on one vertex. How many diagonals can you draw in an octagon, that all begin at one vertex?

The answer to that question is five. Take a look at the diagram below:

In this diagram I've chosen the diagonal to the left just below the top vertex, and I've drawn diagonals to every vertex that I can draw a diagonal to. Which diagonals can't I draw diagonals to? Well, I can't draw a diagonal from a vertex back to itself, and I can't draw diagonals to the two vertices next to that one (because those wouldn't be diagonals; they'd be sides!).

So there are three vertices I can't draw diagonals to from that vertex. Eight vertices total, minus the three I can't draw to, leaves five. That's important to remember: subtract 3 from the number of vertices, and you have the number of diagonals you can draw from any vertex.

But that's just one vertex! You could draw diagonals from any vertex, right? Sure! And there are eight vertices in our octagon, so we take the number of diagonals per vertex, and multiply it by the number of vertices: 5 x 8 = 40.

You might be tempted to think that that's our answer, but it's not. Why not? Because we've counted every diagonal twice! Every diagonal has two vertices, so we've counted it from one end, and we've also counted it from the other end. So to get the actual number of diagonals, we have to divide our answer by 2. 40 / 2 = 20. There are twenty diagonals in an octagon.

Let's try that reasoning on a polygon that has 2000 sides. Now, I'm not going to draw a 2000-gon for you; we'll just have to work out the reasoning without a picture.

1. Pick a vertex. How many diagonals can you draw from that vertex? Answer: 2000 - 3 = 1997.
2. How many vertices total? Answer: 2000
3. How many diagonals counted from all the vertices? Answer: 1997 x 2000 = 3,994,000
4. Oops! We've counted each diagonal twice! How do we get rid of the duplicates? Answer: 3994000 / 2 = 1,997,000

So a 2000-gon has 1,997,000 diagonals!

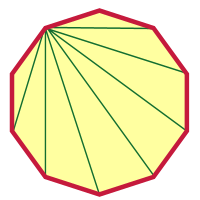
After doing something as crazy as a 2000-gon, a decagon shouldn't seem so difficult, right? I'll get you started, and you can finish it from here. I picked a vertex and drew diagonals from that vertex.

How many are there? Were you able to figure out how many there were without looking at the picture?

Can you figure it out from here? I hope so! Good luck, Alice. 

By the way, there is a formula you can use; it looks like this: D = n(n - 3)/2. But honestly, I don't expect my students to memorize it. I expect them to remember how we reason it out here. If you understand the logic, it's even better than having a formula!