Amelia from Georgia asks, "What do time signatures in music mean?"

Great question, Amelia. I'm going to give you a little more info than you asked for; I'm going to give an answer to your question, and then I'm going to give you some examples of some unusual time signatures in musical compositions.

A time signature is a pair of numbers that you'll see, always at the beginning of a piece of sheet music, and sometimes in the middle of the sheet music as well, since some musical compositions have more than one time signature. Here's an example of a fairly common time signature in the picture to the left.

What exactly do these numbers mean? Well, the bottom number means that a quarter note gets a beat, and there are three beats in a measure. That may or may not help you understand, depending on what music terminology you understand, so let's break that down a bit.

A Beat is the basic unit of time in music. It's like the pulse, or the heartbeat, of a piece of music. If you're clapping along with a piece of music, then there's a good chance you're clapping on the beats. If you're tapping your feet, you're doing the same. If you hear a band playing, and they start off by saying, "1 2 3 4" before they start playing, that counting is helping to set the heartbeat of the music. If you're listening to a drummer, you'll probably hear drum strikes that aren't on the beat, but you'll definitely hear the kick and the snare on the beats. The underlying pattern in most songs is kick-snare-kick-snare over and over again (with other things mixed in). that kick-snare pattern is what sets your toes tapping.

A Measure can be thought of as another unit of time in music; a measure is a set or group of beats. In most music, every measure has the same number of beats, and the first beat in a group gets more emphasis than the others. Sometimes a beat in the middle of the measure will get some emphasis as well. Going back to our example of the kick-snare-kick-snare, that bass drum kick is the emphasis (you could think of it as KICK-snare-Kick-snare/KICK-snare-Kick-snare/etc.), and it repeats over and over throughout the song. In music, measures are defined by a vertical bar right through the middle of the musical staff, like this:

You can see those vertical lines before the words "world," "Lord," "come" and the second syllable of "receive." Those lines mark of groups of beats. And if you were to sing this song aloud, you would realize that the words (or syllables) immediately following those vertical lines are the ones that receive the stress or accent.

We have one more thing we need to explain in order to fully understand a time signature...note names. Take a look at the chart below:

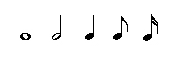
In this chart, the notes, from left to right, are: "whole note," "half note," "quarter note," "eighth note," and "sixteenth note." Why are they called those? Because in the most common time signature (4/4 time), a whole note takes up a WHOLE measure, a half note is HALF of a measure, and a quarter note is one QUARTER of the measure. Of course, if you're not in 4/4 time, that's not true, but the name has stuck. So if you see a 4 in the bottom of a time signature that means a quarter note gets one beat. If you see a 2 in the bottom of the time signature, that means a half note gets one beat. If you see an 8 in the bottom of the time signature, that means an eighth note gets one beat.

Okay, with all of that behind us, let's go back to the original example of 3/4 time. The three means that there are three beats in a measure, and the four means that a quarter note gets a beat. So if you were clapping this one, you would do "CLAP-clap-clap-CLAP-clap-clap," and each "big" clap is the beginning of a new measure. If you were playing the drums, you might play "KICK-snare-snare-KICK-snare-snare."

Interesting Time Signatures

The majority of music you'll listen to is written in 4/4 time (four beats per measure, a quarter note gets a beat). Some will be 3/4 (which is often referred to as a waltz), or 6/8 time (six beats per measure, an eighth note gets a beat - this is the common meter for Irish jigs). Once in awhile you'll hear something that's a bit different.and I've selected a few that you can listen to on youtube.

Of the Father's Love Begotten - since I've already brought up a Christmas song, here's another - an old old Christmas hymn. If you look at sheet music for this one, you'll likely find that the publisher hasn't even bothered trying to put a time signature on it, and has more-or-less given up on doing measure markings; the measure markings are actually just phrase markings, and every phrase is a different length. The link I've provided has no singing, but does show the sheet music.

Waltz from Tchaikovsky Symphony #6 - This one is called a waltz, but it is not in the normal 3/4 time; it's in 5/4 time instead. This means that it has 5 beats in a measure, which gives it a slightly off-kilter feeling because our brains aren't used to processing that kind of rhythm. It's a beautiful, elegant piece of music.

Finale from Stravinsky's Firebird Suite - My introduction to this piece of music was in high school when I participated in the All-State music festival. In the linked video, the section in an unusual time signature starts at 2:00, but it's interesting to listen to the lead-in to that, so it's worth listening to the whole video. The unusual time signature is 7/4 time. I remember looking at the sheet music and thinking, "What in the world?" because every measure was subdivided into groups of 3 beats and 4 beats - presumably to help us get the count right! 

The Dargason from Holst's Saint Paul Suite - This one I played in university orchestra, and oh, was it fun! What makes this piece so unusual is that there are two melodies going on simultaneously, and they are in different time signatures. One melody is "Greensleeves," which is in 3/4 time, and the other is a jig, which is in 6/8 time. Now, as a mathematician, I notice that these two fractions - 3/4 and 6/8 are equivalent. This means that the measure marks fall in the same place for each melody, but what happens in the middle of the measure is quite different.

Here Comes the Sun - In general, the Beatles were notorious for shifting into unusual beat patterns. I've picked "Here Comes the Sun" as an example. You can feel the 4/4 beat through most of the song, but when they get to the bridge, everything seems to go haywire. I haven't looked at the sheet music for this one, but Wikipedia says that the bridge goes through the following rhythm structure: 11/8 + 4/4 + 7/8.

Every year that I teach Physics I run into a small problem with the labs my students do. Here's the problem. My students will collect data (and the issue happens most often when they're timing something) and then they'll look at their data and say, "Wow! One of those points is way off from the others!"

For example, their data points might be the following times in seconds: 4.2, 4.6, 4.3, 4.8, 7.2, 3.9

As they look at those data points, they'll recognize that most of them are in the vicinity of 3.9 to 4.8, but there's one value (7.2) that is way off from the others. Obviously something went drastically wrong with that trial!

So what do I tell them? I'd like to tell them, "Use your statistics knowledge to determine the outliers." Outliers are points like 7.2, which are clearly outside the reasonable range. That's what I'd like to tell them, but I don't, because I know perfectly well that many high school science students have not yet learned enough statistics to calculate outliers.

And I have no intention of spending my Physics class time teaching statistics!

So what do I do? I say to them, "If it looks ridiculous, dump it."

Now, that's a quick approach, and it saves a lot of time, but it's not really a "good" approach (although I'm not the only science teacher that does it!). Why is not a good approach? Because good scientists try to avoid using intuition and guesswork when selecting their data. That kind of fuzzy thinking can result in people massaging their data to make it say exactly what they want it to say.

So this year, I decided it was time to resolve that problem. Not by teaching my students how to find quartiles, interquartile ranges, and outliers. No...I decided to create a calculator that they could enter their data in, and have the calculator list their outliers.

And, while I was at it, since I realize these kinds of tools can be very helpful for both teachers and students, a whole section of statistics calculators was added to the site. These include calculators for various means (arithmetic, geometric, and harmonic), as well, as standard deviation, variance, and other useful statistical quantities.

You can find the calculators here: Professor Puzzler's Statistics Calculators.

Twelfth grader Abbey wants some help with the following: "Factor x⁶ +2x⁵ - 4x⁴ - 8x³ + x² - 4."

Well, Abbey, if you've read our unit on factoring higher degree polynomials, and especially our sections on grouping terms and aggressive grouping, you probably realize that a good way to attack this problem is to try grouping the terms. Hopefully, you tried something along those lines. Here's one method (I'll get you started on another method at the end of this post):

(x⁶ + 2x⁵) - (4x⁴ + 8x³) + (x² - 4).

That looks promising, since every group can be factored:

x⁵(x + 2) - 4x³(x + 2) + (x - 2)(x + 2).

Great! every group has an (x + 2) term in it, so we can factor that out:

(x + 2)(x⁵ - 4x³ + x - 2)

I'm going to attempt grouping on that second polynomial:

(x + 2)[(x⁵ - 4x³) + (x - 2)]

(x + 2)[x³(x² - 4) + (x - 2)]

(x + 2)[x³(x - 2)(x + 2) + (x - 2)]

And once again we have a common factor in our groups - this time it's (x - 2).

(x + 2)(x - 2)[x³(x + 2) + 1]

(x + 2)(x - 2)(x⁴ + 2x³ + 1)

Now we have something that can't easily be grouped, because it has 3 terms. So I decided to try something crazy: I added in x² and subtracted it back out again. Why? Take a look:

(x + 2)(x - 2)(x⁴ + 2x³ + x² + 1 - x²)

(x + 2)(x - 2)[(x⁴ + 2x³ + x²) - (x²- 1)]

(x + 2)(x - 2)[x²(x² +2x + 1) - (x + 1)(x - 1)]

(x + 2)(x - 2)[x²(x + 1)² - (x + 1)(x - 1)]

My groups each contain an (x + 1), so I can factor that out:

(x + 2)(x - 2)(x + 1)[x²(x + 1) - (x - 1)]

(x + 2)(x - 2)(x + 1)(x³ +x² - x + 1)

At this point, I tried a couple different groupings, and nothing seemed to work to factor (x³ +x² - x + 1). That doesn't mean it's not factorable, but I got a little suspicious, so I pulled out the Rational Root Theorem, which tells me that if that thing has any rational zeroes, they have to be either 1 or -1. Since neither of those are zeroes of the polynomial, that means it's unfactorable over the rationals. Therefore, the final answer is:

(x + 2)(x - 2)(x + 1)(x³ +x² - x + 1)

Just a couple notes on this, before I'm done:

1. I enjoy the process of trying to do grouping (and what I call "aggressive grouping") on polynomials in order to factor them. I think it's a good mental exercise. Nevertheless, I should point out that according to the Rational Root Theorem, if this polynomial has any rational zeroes, they are any of the following: -1, 1, -2, 2, -4, 4. Trying out those to see which work, and then using Synthetic Division to divide out the factors will guarantee you a solution, even if you can't figure out groupings to do.
2. There's another way to start off the problem (which is actually what I did the first time I solved the problem), which involves rearranging the terms before grouping: (x⁶  - 4x⁴) + (2x⁵- 8x³) + (x² - 4). Grouping this way has the advantage of pulling out (x + 2)(x - 2) all in one step, and going straight to a 4th degree polynomial. It's nice to see that the problem can be done in multiple ways, don't you think?

Second grader Phushisa from Thailand asks this question: "What is your favourite song?"

Thank you for asking that question, Phushisa! Normally I get asked questions about math, or about poetry, or science, and I don't usually get to talk about myself, so this is a fun question.

Before I begin, I should point out that there is a huge amount of music in this world, and I really love a lot of it, and listen to a lot of it, and it would be almost impossible to pick on single song. In fact, my favorite song varies from day to day and time to time, depending on my circumstances, my mood, etc.

So I'm not going to pick one single favorite. I hope that's okay.

Also, I'm going to stretch the definition of "song," because I'm a big fan of orchestral music - symphonies, concertos, and so forth. And no one calls those things "songs" - they call them "pieces" or "compositions" or (of course) "symphonies" and "concertos".

If I'm doing computer work, or preparing lessons for school, I don't really want my brain actively engaged in the music, so I will rarely listen to music with words. This is when I spend time listening to "classical" music. (I put the word "classical" in quotes because "classical" is an era of musical composition, but outside of the music education and performance community, people use the word "classical" to describe any orchestral or operatic music.)

Speaking of which, I'm not a fan of opera, just to get that settled.

So here are a couple of the pieces of orchestral music that I most love:

Tchaikovsky's Symphony #5
This is the one that I give as my standard answer when someone asks "What's your favorite symphony?" In general, I love anything by Peter Tchaikovsky, but this one tops the list for me. There are some absolutely beautiful, lyrical sections, and some sections that are full of drama and intensity. The last movement (section) keeps building and building, and just when you think it's almost done, it keeps building some more. If you'd like to hear it, there's a recording on YouTube of Leonard Bernstein conducting it. If you don't have time to listen to the whole thing, jump to the last five minutes, and watch how insanely excited Bernstein gets while conducting. It's worth a few minutes of your time.

Khatchaturian's Symphonic Poem #3
This thing is what I listen to when I feel like getting a little more modern. Aram Khatchaturian's music sometimes seems a bit discordant, and off-kilter, but for sheer power and drama, it's pretty amazing. This piece of music has an organ as one of the instruments, and the organist's fingers have to be flying across the console. I think it must be a very challenging piece for the entire orchestra, because I've listened to several recordings of it, and none of them sound at all like the others. My favorite is the Chandros recording, which can be found on YouTube as well. One commenter described the end of the piece as "insane, pure musical carnage," Good description.

If I'm not working, I'm more likely to want music with lyrics (singing), and there's so much music out there that rather than picking a favorite song, can I pick a favorite musician? I promise, it'll be interesting, because he's a musician most people I know haven't even haven't heard of. His name is...

Andrew Peterson
Peterson is what I would consider to be a real wordsmith. His use of language, metaphor, rhythm and rhyme ranges from elegant to almost comical, depending on what he's trying to say, and what he's trying to say is usually very thought provoking (even when he's funny). He's a master of slant rhymes and unexpected rhymes. I remember listening to one of his songs and hearing this line: "We've got Andy on the guitar 'cause I promised him Some Texas barbecue." And every time I heard that line, I felt like it was a pair of lines that rhymed, yet for the life of me I couldn't figure out why, because there are no rhyming words in there. Finally, I realized that the rhyme was the second syllable of "guitar" with the first syllable of "barbecue" ("tar" with "bar"). And I thought, "Who in the world comes up with something as crazy as that, and makes it work?"

And the answer is, obviously, "Andrew Peterson."

Have you ever noticed that sometimes you'll hear a song and really love it right off the bat, but gradually get tired of it? Peterson has the opposite effect on me; it usually takes me a few listens to really appreciate it musically and lyrically, but then it just keeps growing on me, and I don't tire of it easily.

Favorites? My wife says that one of her favorites from Peterson's most recent album is "Be Kind to Yourself," which Peterson wrote for his teenaged daughter (and then sang with her, which you can watch/listen to in the video linked).

From the same album, one of my favorites is "The Rain Keeps Falling," which is about finding both peace and hope for the future in the troubles of life. I'd also add this one, which has a similar theme: "The Sower's Song." If you listen to this one, pay attention to the percussion underlying the words. Usually the drummer gets to show his stuff during the pauses between lyrics (that's why they call them drum fills - because they fill the gaps between lines of words), but toward the end of this song there are some really interesting things happening with percussion that builds in intensity during the line of singing.

I hope you enjoy some of this music as much as I do!

"Can the context of a word change the way its syllables are stressed/unstressed? Myra"

Yes, Myra, the context can definitely change the way we stress the syllables. Here's a simple example:

"I would never desert you in the desert."

How did you stress the syllables in the word "desert"? Hopefully, the first time the word showed up, you pronounced it "de-SERT," with the stress (accent) on the second syllable. But what about the second appearance of the word? You didn't pronounce it the same way, did you? You pronounced it "DES-ert," with the accent on the first syllable.

The difference, of course, is that even though they are spelled the same, these are two quite different words. One of them is a verb, that means to abandon, and the second is a noun -- a dry and barren landscape.

There are occasions when a single word functions as either a noun or an adjective, depending on the context, and the difference in part of speech is reflected in the way it is pronounced. For example, consider the word "arithmetic." Is it a noun? Or is it an adjective? It actually could be either, depending on the context.

"I really enjoy studying arithmetic."

In this case, "arithmetic" is a noun, a branch of mathematics, and we pronounce it "a-RITH-me-TIC," with the primary accent on RITH, and a secondary accent on TIC.

"I really enjoyed studying an arithmetic sequence."

In this case, "arithmetic" is an adjective rather than a noun; it is describing a type of sequence. As an adjective, the word is pronounced "A-rith-ME-tic," with the stresses inverted from the noun pronunciation.

Can you think of other words that have different pronunciations depending on the context?

Incidentally, there's another way that context can affect how syllables are stressed. Sometimes, the innate rhythm of a phrase we're saying can lead to slight variations in accent. I emphasize here the word slight.

Here's one example. I mentioned the word "sequence" above; let's take that word and make it plural: "sequences." If you pronounce this word, you will likely pronounce it like this: "SEQ-uenc-es," with primary stress on the first syllable, and no secondary stress. I checked a phonetic spelling in an online dictionary, and that is exactly what it showed.

So now let's take the phrase "arithmetic sequence" and make it plural: "arithmetic sequences."

How do you pronounce this? The answer (I love combining math and poetry) is that you pronounce it iambically, which means you pronounce it with alternating unstressed and stressed syllables: "A-rith-Met-ic SEQ-uenc-ES."

Your sense of rhythm almost begs you to put a secondary stress on that final syllable. Now, as I said, it's very slight, and maybe you don't add that extra stress yourself, but I can tell you, as a math teacher, I hear that extra accent all the time. The same is true for the phrase "geometric sequences."

The same thing happens (for essentially the same reason) when we read poetry. Say the word "happy" and ask yourself where the stress is. Presumably you said that it comes on the first syllable: "HAPP-y."

But now read these very familiar lines of poetry: 

But I heard him exclaim, 'ere he drove out of sight,
"Happy Christmas to all, and to all a good night!"

Did you notice what happened? Your brain subconsciously (or maybe consciously) got so wrapped up in the rhythm of unstressed/unstressed/STRESSED over and over again that you really didn't give stress to either syllable of "happy," waiting instead to punch the first syllable of "Christmas."

In fact, that's precisely what the author intended you to do; it is a form of poetry called "anapestic tetrameter," in which every stressed syllable is preceded by two unstressed syllables. And those two unstressed syllables are the word "happy."

Related post: How to recognize stressed and unstressed syllables.