9th grader Akhil from Kerala asks the following: "The sides of a quadrilateral are extended to form exterior angles. Find the sum of these exterior angles."

Hi Akhil, instead of just answering the question you asked, I'd like to explore the question in a little more depth, and explain why the answer is what it is. After all, if I just told you the answer, that would make for a pretty boring blog post!

So let's start off with a quadrilateral. I'm going to show you a picture of one below, and ask a question about it. How many degrees are there in the measures of all the interior angles of the quadrilateral?

Now, you might already know the answer to that question; the sum of all the interior angles is 360 degrees. But can you prove that to be true? It's actually not hard to understand why that quadrilateral (and all quadrilaterals, for that matter) have an interior angle sum of 360 degrees. To see why, just look at this picture, in which I've divided the quadrilateral into triangles:

How many triangles did it take to divide up that quadrilateral? It took two, right? And how many degrees does each of those triangles have? 180 degrees. And so altogether, how many degrees do they have in total? 180 x 2 = 360 degrees.

Understanding that the total of the interior angles is 360 degrees is important to finding the number of degrees in the exterior angles. Here's a picture that shows what you described - the sides being extended to form exterior angles:

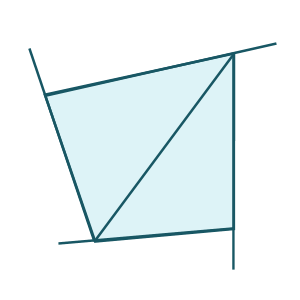
By extending these sides, we've created linear pairs - pairs of angles that form a straight line. Each linear pair includes an interior angle and an exterior angle. Each linear pair adds to 180 degrees (a straight line), and there are four linear pairs (because there are four sides).

So if there are 4 linear pairs, and each linear pair is 180 degrees, that's a total of 720 degrees. But 360 degrees of that is interior angles, so the exterior angles have to add up to 720 - 360 = 360 degrees! And that's your answer.

Now, it might be tempting to think that the interior angles of a polygon and the exterior angles of a polygon will always match, since they do in the case of a quadrilateral, but that is not the case. Let's take a look at a pentagon to see why. Here I'll give you a pentagon divided into triangles, and with sides extended:

In the case of a pentagon, we can divide the polygon into 3 triangles, which means the interior angles add to 3 x 180 = 540 degrees.

We've created 5 linear pairs, which total 5 x 180 = 900 degrees.

Since there are 900 degrees total, and the interior angles add to 540 degrees, the sum of the exterior angles is 900 - 540 = 360 degrees!

It turns out that the sum of the exterior angles is 360 degrees regardless of whether it's a quadrilateral or a pentagon.

What do you think...can you generalize it even further? How many degrees are there in the interior of an n-gon? And how many degrees in the exterior angles of an n-gon? I'll leave it to you to figure that out. Thanks for asking, Akhil!

Emmanuel from Papua New Guinea asks, "How do find the common ratio of a geometric sequence if the ratio of the fourth and second term are given?"

Well, Emmanue, the short answer is: you can't!

Let's suppose the second term of geometric is 4, and the fourth term is 16. You might think, "Oh, that's easy - the ratio must be 2, because 4 x 2 is 8, and 8 x 2 = 16!" But that's not necessarily true - maybe the ratio is -2! 4 x -2 = -8, and -8 x -2 = 16. 

The problem is, in a geometric sequence, all the even-numbered terms will have the same sign, but that won't tell us anything about the sign of the odd-numbered terms, and that information is needed to find the ratio. But we can set up an equation that'll give us the possible values.

Let's say the second term is 2, and the fourth term is 18. Then 

ar = 2, and ar³ = 18

If we rewrite the second equation as ar(r²) = 18 we can subsitute the first equation in place of ar, giving:

2r² = 18, or 

r² = 9.

Now, it's tempting at this point to say, if r squared is 9, then r must be 3, but you're missing a possibility if you do that, because 9 has two square roots: 3 and -3. These are your two possible ratios. We don't know what the ratio is, but at least we've narrowed it down to two possibilities!

By the way, as a side note, in order to get my students to avoid missing a solution in an equation like r² = 9, I tell them they have to solve the equation like this:

r² = 9
r² - 9 = 0
(r - 3)(r + 3) = 0

Therefore r - 3 = 0 or r + 3 = 0, which leads to r =3 or r = -3.

It's more work, but it keeps them (most of the time) from forgetting a root!

First of all...sorry about the click-bait title for this post. You'll see why in a minute.

Second...today I'm not answering a question from a visitor; I'm putting on my cranky-old-man hat and griping about something that concerns me deeply. 

Yesterday New York Times had an article in which President-Elect Trump's aides said that he was considering (once in office) spending his weekdays at the White House, but on the weekends living at either his Trump Tower, his golf course in NJ, or his Mar-a-Lago estate.

OccupyDemocrats then did what any good clickbait site would do - they grabbed a couple sentences from the news report, built conclusions from it, and gave it a sensational (and inaccurate) headline: "Trump just announced he won't live in the white house full time, wants to golf and relax."

If you don't see a difference between what NYT reported and what OD reported, think it through very carefully - I think you'll see that there are important differences. NYT said  it's what he's considering; OD said it's what he has announced. NYT simply stated where he was considering living on the weekends; OD made assumptions about what he would do while he was there. To make it even better, they found a nice picture of Mr. Trump golfing, to help add to the overall impression of the headline.

Certainly, I think it's possible, based on all that we know of him, that Donald Trump may be expecting to take a vacation every weekend, but that is not what his staff said, and to declare it as fact is nothing short of dishonest.

Of course, OccupyDemocrats is not alone in this kind of non-reporting. ConservativeTribune, WesternJournalism, USUncut, and many others, are guilty of this as well. The prevailing idea of journalism seems to be: find a news report on a "respected" news site, grab a sentence or two out of context, sensationalize it, and then give it an even more sensational headline in order to get people to click-through from social media. 

I used to waste so much time reading Conservative Tribune articles my friends shared on social media, and researching the context of whoever they quoted, so I could tell my friends whether the article was false. Eventually, I realized that, for my own sanity, I needed to block this site from my facebook feed (notice, by the way, that I refuse to call it a newsfeed). I haven't seen a CT article in months, and I consider my life to be very much enriched for the lack.

So here's where things get really ugly, because we're going to talk about site popularity. A few weeks ago, Alexa.com posted in their statistics that this site (TheProblemSite.com) has broken into the top 100,000 most popular sites in the country. Using the estimate that there are a billion websites in the world, this puts us in the 99.99 percentile among US web users. I was pretty excited about that. But...that same site puts OccupyDemocrats in the top 1000 (99.9999 percentile), and ConservativeTribune at...are you ready for this? #52. There are only 51 websites in the world that are more popular than CT among US visitors, according to Alexa. That puts them at 99.999995 percentile. 

Alexa says that CT has about 1.8 million visitors every day, and about 100 million page views every month.

In one month, CT gets 19.2 million UNIQUE visitors (96.7% of which are from the US). Unique means, if I visit twice in one month, I only get counted once. So about 6% of the US total population is visiting CT each month, and presumably assuming they've received a dose of news for the day. That's just ONE of these sites. What do you suppose the percent would be if we included ALL the sites like that (both the conservative ones and the liberal ones), and not just CT?

And that's just the people who actually click a link somewhere to visit their site. How often have you scanned your facebook feed and seen a headline from one of these sites and moved on without clicking? You're a person who has been "reached" by one of those sites, who does not count in their "reach" statistics. Did you assume you were looking at a news headline when you scrolled past it? Did you assume it must be true? 

We complain all the time about "the media," but we don't have a whole lot to complain about if we're getting our news from entertainment sites instead of news sites. It's not much wonder we've become so divided and divisive if, after choosing sides, we gravitate toward the most extreme and dishonest sources to get our information.

I get that all news sources are biased, in the sense that they don't just give us facts, they also make choices about which facts are significant enough to be reported, and also give analysis of what they think the facts "mean" in the grand scheme of things. But biased is a whole different league from un-fact-checked click-bait that exists to serve as an echo chamber for people who already know what they think about everything.

Let's make a commitment. It's not easy, but it's only three steps:

1. Begin a daily mantra: "I saw it on social media, so it's probably not true. I saw it on social media, so it's probably not true. I saw it on social media, so..."
2. Every time you see a new "news" source, carefully research the first three articles you see from them, and if you can find even one blatantly dishonest statement in those articles, block the site from your social media.
3. At the same time, explain to your friend WHY you're blocking the site they just shared. To make it easy, of course, you're welcome to share this article - we won't complain!

The truth is, sites like this aren't breaking the internet; they are breaking the nature of political discourse, and we are complicit. Yes, they are culpable, but so are we, every time we mistake an entertainment site for a news site. Let's start doing better.

Update, Nov 15, 2016 Cheyanne wanted some elaboration on #2 - How do you fact check? What do you compare to, considering how biased everything is? Here is my response to her:

 There are a few different things you can do. In the case of the example above, I went to NYT, which is the site that OD quoted, and it was easy to see that they were simply taking what NYT reported and misrepresenting it. That's not to say NYT ISN'T biased, but when you find a site that deliberately misrepresents what they've said, you know that site isn't just biased, but downright dishonest.

Also, I often find articles that have short snippets of speeches, and I'm always suspicious, and go find a transcript (or video) of the ENTIRE speech, so I can find the quote in context, to see if the site is treating it fairly. For example, the number of times I've found conservative click-bait sites guilty of deliberately taking Obama quotes out of context is both embarrassing (speaking as a conservative) and appalling (speaking as a human being who cares about truth).

I also make use of custom date searches in search engines. For example, recently, there's been this thing floating around that Kurt Cobain predicted the rise of Trump. I grabbed a phrase from the supposed Cobain quote and put it into google, with quotes about it. Then I clicked the "tools" link, and "Custom date Range" to tell it I only want results from Jan 2000 - Dec 2014. Google tells me there are no results. Turns out that quote first showed up in 2015, which is a problem for Cobain, who has been dead since 1994.

Question: an arithmetic mean of two numbers is always between the two numbers being averaged. Is this also true of harmonic means and geometric means?

Yes, it is. Let's take a look at both types of means, and see if we can figure out why. In each case we'll make the assumption that we're taking the mean of two positive, distinct numbers. Positive, because goeometric means and harmonic means are generally defined to be over the set of positive reals, and distinct, because having non-distinct numbers makes the mean equal to the original number, which isn't terribly interesting.

Geometric Mean

The geometric mean is the square root of the product of the two numbers. So if the numbers are a and b, then the geometric mean is SQR{ab}.

We will say, without loss of generality, that the two numbers are a and b, with a < b.

Multiply both sides of the equation by b:

ab < b²

Taking the square root of both sides gives SQR{ab} < b

Similarly, if we multiply the first equation by a, we get:

a² < ab, or a < SQR{ab}

Therefore, a < geometric mean < b.

Harmonic Mean

The harmonic mean is the reciprocal of the average of the reciprocals, or 2ab/(a + b). Again, we'll assume, without loss of generality that a < b.

Multiply both sides of this equation by a, and then add ab:

a² + ab < 2ab

Now factor the left side:

a(a + b) < 2ab.

Finally, divide both sides by (a + b):

a < 2ab/(a + b).

We can repeat the process on the other side:

a < b
ab < b²
ab + ab < b² + ab
2ab < b(a + b)
2ab/(a + b) < b

Therefore, a < harmonic mean < b

Deepak from Kanpur, India, asks the following question (edited for clarity):

In the sentence "I am a good writer," how does the meaning change based on which word you emphasize?

Well, Deepak, that's a great question! It turns out that you could say this sentence in several different ways, and each way of emphasizing the words gives a slight tweak to the meaning. To answer you, I'll mark the word that's emphasized by marking it off with asterisks. Beneath each sentence, I'll provide an explanation. In each case, the emphasis implies that the speaker is, in some way, disagreeing with what a previous speaker has said.

*I* am a good writer.
This sentence, with the emphasis on the subject, suggests that someone has previously made a statement implying that it was someone else who is a good writer. For example, if someone is comparing you to Mark, and says that Mark is a good writer, you would emphasize "I" to indicate that you're disagreeing with their conclusion is wrong about which of you is a good writer.

I *am* a good writer.
In this case, it's the verb you are emphasizing. What's the opposite of being a good writer? NOT being a good writer. So presumably, someone just told you that you are not a good writer, so you emphasize "am" in order to disagree with them.

I am *a* good writer.
Emphasizing an indefinite article like "a" is a strange choice under most circumstances, but I can imagine a circumstance where you might do that. You have just published your first novel, and an adoring (and maybe slightly crazy) fan says to you that you are "THE good writer." In other words, suggesting (hyperbolically) that you are the only good writer in the whole world. You disagree with that designation, and graciously point out to your fan that you are only one of many good writers.

I am a *good* writer.
Here you emphasized an adjective. So maybe someone just used a different adjective to describe your writing skills. Maybe they said, "You're a fantastic writer," and you wanted to dampen their enthusiasm by indicating that you're just good, but not fantastic. Or maybe they said you're a lousy writer, and you want to defend your skills by saying that you're a good writer.

I am a good *writer*.
In this case, it's likely that someone said that you're good at something else. Maybe they thought you illustrate children's books, when in reality you write them. Or maybe they thought you were a carpenter, but you're actually not. However, the fact that your sentence has the word "good" in it, suggests that the person speaking thought you were good at whatever it was that they thought you do. "You're a good illustrator." "No, I'm a good WRITER." 

And there you have it - a five word sentence, with five different ways of emphasizing the words! Each one has a slightly different meaning, because each one is a response to a slightly different situation. And if there is no surrounding context - if you were just announcing this into the silence - you probably wouldn't emphasize any of the words.