An anonymous reader asks, "How do you get good at 'listening' for iambic pentameters?"

Poetry, like music, has rhythm. In music, the rhythm is established using a few different intstruments. In a band, the drummer and the bass guitarist are the primary rhythm-holders. Those deep, bassy sounds like the guitar and the kick (bass) drum set our subwoofers to vibrating, and mimic our own heart rhythms.  In some music, the rhythm is prominently defined by the kick drum and the snare drum. A GEICO ad from awhile back made this point with a pig singing "Boots and pants and boots and pants and..."

The words "boots" and "pants" represent the kick drum*, and the word "and" represents the snare. The kick drum provides the primary driving beat, and the snare represents what we call the "off-beat".

So the pig is actually giving you the beat of a song.

You can feel the rhythm of that if you repeat it over and over, and if you do it just right, it's almost indistinguishable from a techno band.

The rhythm of a poem (in poetry, we call it the "meter" of the poem) can be understood in terms of kick drums and snares, which means it can also be understood in terms of phrases like "boots-and-pants-and". In poetry, we have stressed syllables and unstressed syllables. Stressed syllables correspond to the driving "kick" beat, and the unstressed syllables correspond to the off-beat of the snare. So what does iambic pentameter look like?

and-BOOTS-and-PANTS-and-BOOTS-and-PANTS-and-BOOTS.

Notice that we start with the snare, or the off-beat, and we end with the kick. Also notice that we have 5 kick beats. This is why it's called penta-meter; "penta" is five and "meter" is rhythm, so pentameter is a five-rhythm.

The nice thing about having five kicks in a line is that you've got five fingers on one hand, so while you are saying "and boots and pants..." each time you say either "boots" or "pants" you can tap a finger on the table, and when you've tapped all five fingers, you've completed a line of the rhythm. So if you want to get good at listening for iambic pentameter, do this repeatedly. Say the "and-boots" pattern while tapping out the kick beat on your fingers. If you want, after you do the fifth finger, give a little pause, and then start all over again:

and-BOOTS-and-PANTS-and-BOOTS-and-PANTS-and-BOOTS [pause] and-BOOTS-and-PANTS-and-BOOTS-and-PANTS-and-BOOTS [pause] etc.

After awhile, that rhythm will get ingrained in you, and you'll be doing it without even thinking about it. Now let's take a look at something that's written in iambic pentameter:

The quality of mercy is not strain'd,
It droppeth as the gentle rain from heav'n
Upon the place beneath: it is twice blest;
It blesseth him that gives and him that takes. (Shakespeare, The Merchant of Venice)

If you've got that "boots-and-pants" thing going through your mind, it'll be easier to see that this is iambic pentameter:

the QUAL i TY of MER cy IS not STRAIN'D
it DROPP eth AS the GEN tle RAIN from HEAV'N
u PON the PLACE be NEATH: it IS twice BLEST;
it BLESS eth HIM that GIVES and HIM that TAKES.

Can you feel the rhythm of it?

Important Disclaimers

1. Thinking "and-boots-and-pants" may be a great way to recognize and understand the rhythm of poetry, but it is NOT a good way to read poetry; nobody wants to hear Shakespeare sounding like techno music**. Instead, you should use boots-and-pants to help you recognize where the beats are, but then once you've understood which syllables get the stress, you're going to read this in your normal reading voice, without giving unnecessary extra accent to any syllables.
2. Also, even though when you practiced the rhythm, you left a pause between lines, you won't necessarily do that when reading a poem. Focus on the meaning of the lines; if a line does not complete a thought, you're not going to pause at the end of it. And if a thought is completed within a line, you're going to pause there. Remember that meaning is most important, and rhythm serves the poem, not the other way around! So with this in mind, the Shakespeare piece would be read like this:

The quality of mercy is not strain'd, [pause]
It droppeth as the gentle rain from heav'n upon the place beneath; [pause]
It is twice blest; [pause]
It blesseth him that gives and him that takes.

Other Meters

The "boots-and-pants" idea can be used to recognize other meters as well. For example, if you want to get the feel for anapestic tetrameter, you should start thinking:

and-the-BOOTS-and-the-PANTS-and-the-BOOTS-and-the-PANTS.

Notice that we've added the word "the" after the word "and" each time. This gives the meter a "triplet" feel. Also note that we only hit four driving beats in a line instead of five. So if you're counting this on your fingers, leave out your thumb.

You can see this rhythm in the well known Christmas poem "Twas the Night Before Christmas":

twas the NIGHT be fore CHRIST mas and ALL through the HOUSE
not a CREA ture was STIRR ing not E ven a MOUSE

* Technically, "boo" and "pan" represent the kick, and the "ts" represents the hi-hat. Thus, we really break it down like this: BOO-ts-and-PAN-ts-and.

** Well, okay, maybe "techno-shakespeare" should be a thing. But I'm not sure your poetry teacher will appreciate it! 

Richard from Los Angeles asks, "What is a von Neumann Machine?"

Hi Richard, a von Neumann machine is a concept for a machine that is self-replicating. This means that it is a machine capable of building another machine just like itself. This idea has been around for quite awhile (there's even an anecdote about Rene Descartes telling Queen Christina of Sweden that the human body is just a machine, and she responded by pointing at a clock and challenging him to make it produce offspring). And that's actually, in a sense, the concept of a von Neumann machine - it's a machine that produces offspring.

So let's take a look at a couple examples of how a von Neumann machine might be used, if we could build one.

Mining Ore

Let's say you built a machine that could mine iron from an asteroid. We'll suppose that it can mine 200,000,000 kg of iron ore per year. If this was a large asteroid (let's say, 10²⁰ kg), it would take 500 million millenia to mine the entire asteroid.

You could build more machines to help speed the process up, but if you built 1000 machines, it would still take 500 thousand millenia to mine it.

So a clever approach would be to build a machine that mines ore, and then uses part of the ore to build another machine just like it. There are trade-offs to this approach, and we'll make some assumptions to help explore those trade-offs.

First, we'll assume that the machine can only mine ore for half the year, because it's spending the other half building a machine.  This means that it can only mine 100,000,000 kg per year instead of 200,000,000 kg.

Second, we'll assume that the machine has to use a quarter of the ore mined to build its "offspring". This means that there's only 75,000,000 kg of ore produced that is actually "produced" each year per machine.

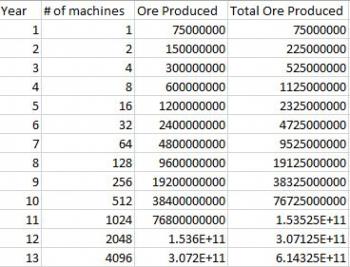
So at the end of the first year, we now have two machines instead of just one. This means that the second year, we can produce 150,000,000 kg or ore. The next year we'll have 4 machines, then 8, etc. After 11 years we'll have just over 1000 machines, and it'll only take 22 years to have over a million mining machines on the asteroid.

Here's a table that shows the first few years. The first column is the year number. The second is the number of machines. The third is the ore produced that year, and the final column is the total ore produced for the entire length of the project (the sum of all the ore production).

Terraforming Mars

Freeman Dyson (known for the Dyson Sphere) proposed that if we want to terraform Mars (make it like earth, so humans can live on it), we're going to need to import massive amounts of water. Where will we get it? Saturn has a moon (Enceladus) which has a very thick crust of pure, clean ice.

So Dyson proposed that we could, theoretically, build a machine which is capable of doing all of the following tasks:

1. mine ice from the surface
2. mine iron ore from the core
3. use the iron ore to replicate itself
4. use the iron ore to also build a simple unmanned spacecraft capable of navigating to Mars
5. load the ice into the craft

Obviously, this machine is going to be very sophisticated. If you think about it, a self-replicating machine is actually an entire factory. And this one is a factory that produces both a mining machine and a flying machine. But if we could do it, the amount of ice we could move to Mars would grow exponentially with each year.

Space Exploration

Why not use this concept for space exploration? Build a space probe that's capable of landing on an asteroid and using the raw materials of that asteroid to create one, or even a thousand copies of itself before heading for the next solar system. Each of those copies heads out in a different direction and repeats the process, and all the while reporting back to planet earth what they see along the way. Considering the massive amount of time it'll take to travel from one solar system to the next, mapping and exploring the galaxy is an absurdly monstrous task, so this is definitely a situation where having the number of probes increasing exponentially would be of great value.

Other Ideas?

What do you think? What are some other ways we could use von Neumann machines?

Twelfth grader Jodi asks, "Hi Professor, if you could help me understand this problem I would highly appreciate it. Problem: An ant starts digging a tunnel. On the 1st day he digs 9m north. The 2nd day he digs 6 m east. The 3rd day he digs 4m south. He continues to dig in this pattern. Question 1: How far will he dig in total? Question 2: How far north from his starting point will he end up?"

Hi Jodi, this is definitely a fun problem. I'm going to answer these two questions, and then I'm going to pose two more questions for you to think about.

Question 1: How far will the ant dig?

Each day the ant digs 2/3 of what he dug the day before. Thus, his total distance is

Eq. 1: D = 9 + 6 + 4 + 8/3 + 16/9 + ...

Now, there are formulas you can use to calculate that sum, and if you're in a Pre-Calculus class (or higher) you probably know those formulas. I'm going to show you how to get that sum without a formula.  I'm going to take the equation and multiply it by 2/3:

Eq. 2: 2/3D = 6 + 4 + 8/3 + 16/9 + 32/27 + ...

Now, if I subtract the second equation from the first one, all but one of the terms on the right hand side of the equation cancel out, and  I get the following:

Eq. 3: D/3 = 9

This leads to D = 27, which is the answer to Question 1. If you want to make sure, pull out a calculator and punch in a bunch of these terms; you'll see that it doesn't take more than 7 or 8 terms for you to start getting close to 27.

Question 2: How far north from his starting point will he end up?

Before we get started, I'd like to point out that the problem seems just a tiny bit ambiguous. There are a couple ways I could read this:

1. The ant digs North, then East, then South, then repeats this pattern, going North, East, South, North, East, South, etc.
2. The ant digs North, then East, then South, then North, then West (completing the compass pattern) before repeating all four directions.

Strictly speaking, interpretation #1 is the precise reading of the problem, but I have a feeling interpretation #2 was intended, so I'm going to go with that one.

To solve this, we treat a distance south as a negative distance, and we look at the odd numbered terms of the original sequence (because the even numbered terms are east/west motions, and don't affect the north/south distance).

Eq 4: D_N = 9 - 4 + 16/9 - 64/81 + ...

This time the common ratio is negative (we know this because the terms are alternating signs). It is -4/9. So you can do the process I did above, multiplying the equation by -4/9 and then subtracting. Or you can use the formula I referred to above, but didn't tell you:

Eq 5: S = a/(1 - r), where a is the first term and r is the ratio.

D_N = 9/(1 - (-4/9)) = 9/(13/9) = 81/13

Question 3: What about the other digging pattern?

We made the assumption that the problem intended for the ant to dig in all four compass directions, but that may not have been the intent. What if the western direction is skipped each time? How does that affect the answer. It definitely makes it more interesting; I think you'll end up needing to treat it as two separate series: D_N and D_S, and then find the difference.

Question 4: What's the total displacement?

Displacement is a word we use a lot in Physics. It's different from the concept of distance (which is how far the ant traveled). Displacement is how far (and in what direction) the ant ended up from where he started, and it's a combination of the distance north, and the distance east. To find that answer, you would need to set up a D_E equation (distance east), and then do the Pythagorean Theorem on D_N and D_E to find the hypotenuse, which is the distance from his starting point to his ending point.

Since displacement is a vector (magnitude and direction) you'd also have to do a bit of trig to find the direction in which the ant ended up from his starting point.

Those are problems I'll leave you to contemplate. Thanks for asking!

Professor Puzzler

Lavinia from Italy writes: "Hi professor. I have just read your post about this year's number (2017). In this post you say that we can write 2017 as a the sum of one cube plus twice another. 2017 = 11³ + 2 · 7³ I was wondering how you managed manage to discover this. Did you use a formula or something? Thanks, Lavinia"

Thanks for asking, Lavinia. For those who missed it, this is a reference to the following blog post: Happy New Year 2017. In this blog post I make mention of the fact Lavinia pointed out:

2017 = 11³ + 2 · 7³

So how did I discover this odd fact? There wasn't a formula. I found it simply by playing around with the numbers to see what interesting things I found. I don't remember exactly what I was doing when I discovered that, but it probably involved a spreadsheet. I probably was thinking, "I wonder what results I'll get if I subtract perfect cubes from 2017!"

So I probably entered the following formula into cell A1 of a spreadsheet:

= ROW()^3 (cube the row number)

And then, in B1 cell put the following formula:

= 2017 - A1

Then I would have used the "fill down" feature to populate a bunch of rows with the results of those calculations:

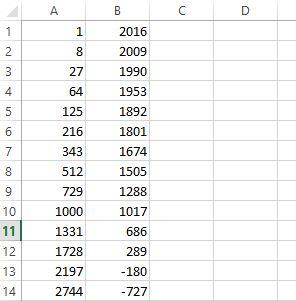
Incidentally, this time as I looked at the rows of numbers, I realized that there's a perfect square in the second column: 289 = 17². So we can also write:

2017 = 12³ + 17²

I probably did something very similar to find the perfect squares that add to 2017:

A1 = ROW()^2
B1 = 2017 - A1
C1 = SQRT(B1)

This would have given the following:

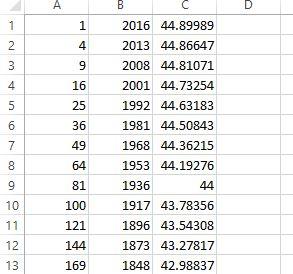
2017 = 9² + 44²

Incidentally, there was another row that had no decimal, further down the spreadsheet. It was row number 44, of course!

Excel (or any other spreadsheet application) can be a great help in exploring mathematical oddities. I realize that I'm a bit spoiled, having calculators and spreadsheets to use when playing with numbers. Imagine trying to figure out quirky number facts like these without even a calculator!

Steve from Cincinnati writes: "I believe this puzzle answer is 1089.

11 X 11 = 4
22 X 22 = 16
33 X 33 = ???

"The first two equations are wrong, but they trick us into looking for a pattern rather than apply the mathematical rules...many people assume an addition function exists between each of the two pairs of integers. Not so. Therefore, thirty three multiplied by thirty three is 1089."

Hi Steve! Of course, you are 100% correct. 33 x 33 = 1089, no matter how many incorrect equations you put before it. Now that I've said that, if I stop there, I've got a really short blog post, and no one wants that - so let's fix their notation in order to turn it into a more interesting puzzle. We'll treat it as a single variable function:

Find x if:

F(11) = 4
F(22) = 16
F(33) = x

It still isn't a very good puzzle, though, because there's not enough information to come up with a single solution. In that respect, it's very similar to the "Squares Problem" I wrote up last year. Here are just three possible answers to the puzzle.

Solution #1
We add the digits of the number in the function's domain, and then square it. (1 + 1)² = 4; (2 + 2)² = 16; (3 + 3)² = 36.

Solution #2
We square the number, and then add the digits: 11² = 121 and 1 + 2 + 1 = 4; 22² = 484 and 4 + 8 + 4 = 16; 33² = 1089 and 1 + 0 + 8 + 9 = 18.

Solution #3
We subtract 8 from the number, and then add the quotient the number and eleven: 11 - 8 + 11/11 = 4; 22 - 8 + 22/11 = 16; 33 - 8 + 33/11 = 28.

I'm sure there are other solutions; those are just the ones that popped into my head on a quick glance. Can you come up with others? Send them my way and I'll add them to this post.