Good morning, and welcome back to school, for those of you who are students! I know that for many of you, school began back in mid-August, but I always think of the day after Labor Day as "Back-to-School" Day - that's just a holdover from my childhood days!

Now that school is back in session, we're starting to get some interesting questions again, so be sure to check back from time to time to see what's new!

A question came to us yesterday from seventh grader Jenny in the Philippines. She wants advice on solving the sort of problem where people are working together. Here's an example of this sort of problem:

Jack and Jill can build a LEGO tower in four hours. If Jack, working by himself, can do the job in five hours, how long would it take Jill to do the job by herself?

First of all, I should point out that this sort of problem always has a built-in assumption that never gets talked about. It's the assumption that the childrens' combined speed of work is equivalent to their individual speeds added together. Depending on the job and the people, this is not necessarily a reasonable assumption. For instance, Jack and Jill could end up getting in each others' way, and therefore slow down the process. Maybe they don't get along well, and fight over how to build the tower. Or maybe they get along quite well, and spend more time talking than building! Often the job in a problem like this will be something like "mowing a lawn," since on a job like that they can work independently and separately, without slowing each other down.

Okay, so we make the assumption that their combined speed is the sum of their individual speeds. In other words, if Jack can build 10 towers per hour, and Jill can build 12 towers per hour, then together they should be able to build 22 towers per hour.

Notice what the units of speed are in this problem: towers per hour. This is a fractional unit, with the number of towers on top, and the number of hours on the bottom.

So we'll say A = Jack's speed, B = Jill's speed, and C = their combined speed

A + B = C

How fast can Jack build a tower by himself? 1 tower every five hours. So A = (1 tower)/(5 hours) = 0.2 towers/hour

How fast can they build a tower together? 1 tower every four hours. So C = (1 tower)/(4 hours) = 0.25 towers/hour

Thus,

0.2 + B = 0.25
B = 0.05 towers/hour

If she builds at a rate of 0.05 t/hr, and we want to know how long it takes to build one tower, our unknown is H, the number of hours:

1 tower = (0.05 t/hr)(H hr)

Divide both sides by 0.05 to obtain: H = 1/0.05 = 20 hours. If Jill works by herself, it'll take her 20 hours to do the job. Does this make sense? Sure! If Jack works by himself it takes him five hours. If Jill helps, it takes four hours, which isn't that much different from Jack's rate, which suggests that Jill works pretty slowly!

So that's the general process, and you can apply that to a wide variety of 'working together' problems. You can even do this with more than two people working together. Thanks for asking, Jenny!

Eleventh grader Kausar asks, "I had this question several times but i do not know how to do it. You are given the 5th and 7th terms of a geometric sequence. Can you determine the 29th term without finding the general term?"

Hi Kausar, the answer to your question is, "Yes, you can." Having said that, I'd like to add that if you'd been asked for the 28th term, or the 30th term, the answer would be "No, you can't." Let's take a look at why.

Let's say the fifth term is 32, and the seventh term is 8. Then we can reason as follows:

"The sixth term is the fifth term times the common ratio, and the seventh term is the sixth term times the common ratio. Therefore, the seventh term is the fifth term times the common ratio squared."

Algebraically, this reasoning looks like this:

a₆ = a₅r; a₇ = a₆r; a₇ = (a₅r)r = a₅r². Thus, 8 = 32r², which leads to r² = 1/4.

Now, without bothering to get the general term, we ask, "How many times would I have to multiply the seventh term by r² to get the 29th term? And the answer is: (29 - 7)/2 = 11.

So a₂₉ = a₇r¹¹ = 8(1/4)¹¹, which is approximately 1.9x10^-6.

So why does this work for the 29th term, but not the 28th? Because (28 - 7)/2 is not an integer, so we can't get there by multiplying by r². We'd have to find r, and multiply by r (28 - 7) times.

So why can't we do that? Well...because the equation r² = 1/4 doesn't have just one solution; it has two. r = 1/2 or r = -1/2. So you have two possible values for the 28th term. 

I occasionally get hired to write problems for math competititions, and one of the "tricks" I'll occasionally pull on students is to give a sequence like this, where students are likely to end up with an equation like r² = 1/4, and then forget that this has two solutions instead of just one. It's amazing how often a simple trick like that will trip students up!

One student asks for an explanation of central angles - how is a central angle different from an inscribed angle?

The best answer to this question is probably a picture (or, rather, a pair of pictures). The first picture shows a circle with center at X. The angle has its center at the center of the circle. Therefore, it's a central angle.

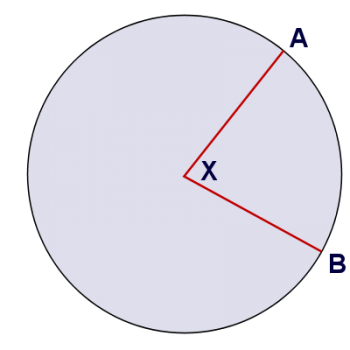
The second picture shows an additional angle, marked in green. This angle is an inscribed angle, because its vertex lies on the circle.

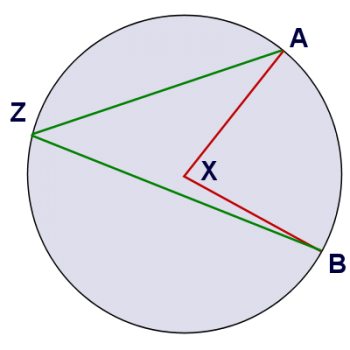
In both cases, the angles cut off the same arc - arc AB. So how are these two angles different? Well, if you look at the picture, you can see pretty easily that an inscribed angle is smaller than a central angle that cuts off the same arc. I think we can prove that the inscribed angle is half the size of the central angle. Want to give it a try?

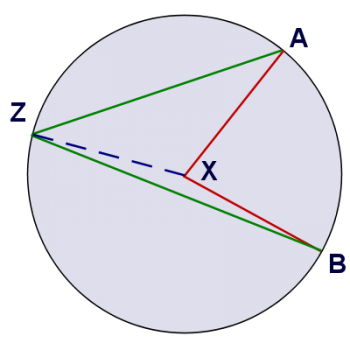
Let's construct a segment from Z to X, which splits the quadrilateral AXBZ into two triangles: AZX and BZX. Both of these triangles are isosceles (because two of their sides are radii of the circle). If we let m be the measure of angle AZX, n be the measure of angle BZX, and k be the measure of the central angle, then we can write the following equation for the sum of all the interior angles of the quadrilateral AXBZ:

(measure of AZB) + (measure of B) + (measure of A) + (measure of X) = 360

(m + n) + (n) + (m) + (360 - k) = 360

2m + 2n + 360 - k = 360

k = 2(m + n)

And since m + n is the measure of AZB, we've shown that the measure of a central angle has twice the measure of any inscribed angle that cuts the same arc. I hope that's helpful!

"Good day sir, pls sir I need explanation on how to solve an equation like this x⁴ - 3x² + 2. although I don't have problem on factorization but I don't know what to do when the power of "X" is greater than 2. looking for your reply Sir"

I can give you several answers to this question. One is a short quick answer that works for this problem. The other answers are more detailed, and give you more information than you need to solve this specific problem. Let's start with the short answer.

Short Answer

Notice that all the exponents in this expression are even. This means that we could do a substitution like this: y = x². Doing this substitution changes the expression to:

y² - 3y +2

As you said, you know what to do when it's a quadratic (the highest exponent is 2). This factors as follows:

(y - 1)(y - 2)

But wait - you're not done, because the problem had x in it, not y, so you have to put the x's back in:

(x² - 1)(x² - 2)

Now that you've substituted x back in, you should realize that one of those can be factored:

(x - 1)(x + 1)(x² - 2). And that's your factorization. Technically, that's your factorization over rationals; if you're including irrationals, the second binomial can be factored as well:

(x - 1)(x + 1)(x - √2)(x + √2)

Longer Answer

The method shown above doesn't just work if the exponents are 4 and 2; they also work if the exponents are 6 and 3, or 10 and 5, or any other such combination. If you wanted to get really ugly, I suppose it would also work if you had fractional exponents like 5 and 5/2.  The method works if it's a trinomial (three terms) and the exponent of the highest degree term is twice the exponent of the middle term, and the lowest degree term is a constant. For example, consider this one:

x⁶ + 8x³ + 12

We'll substitute y = x³.

y² + 8y + 12
(y + 6)(y + 2)
(x³ + 6)(x³ + 2)

Of course, if you were factoring over reals, and you happen to know the rule for factoring a sum of cubes, you could factor this further. But since you mentioned not knowing what to do for exponents larger than two, we can save that for another day!

Similarly, if it was x¹⁰ +8x⁵ + 12, you would do the substitution y = x⁵. 

Longest Answer

Again, this only works for trinomials under certain circumstances. But what if the expression doesn't match those criteria? Let's take an example:

x³ + 5x² - 2x - 10

In this case, we can't do a substitution to simplify it, so we'll try doing some grouping. Since there are four terms, I decide to try breaking it into two groups of two terms each:

(x³ + 5x²) - (2x + 10)

Now we can factor each group:

x²(x + 5) - 2(x + 5)

Oh! Since both binomials in parentheses are the same, we can rewrite this as:

(x² - 2)(x + 5).

This technique sometimes works. Sometimes grouping works only if you get creative in your groupings. Sometimes you need to rearrange the terms. Sometimes you might need to group them into groups of three terms, or groups of four terms.

Here's an example of rearranging terms:

x³ + 3x² + 3x + 1
(x³ + 1) + (3x² + 3x)
(x + 1)(x² - x + 1) + 3x(x + 1) 
(x + 1)(x² + 2x + 1)
(x + 1)³

Confession Time

When I first saw your problem I did not come up with the simple solution. I wasn't paying attention, I guess, and my first thought was: I'll do this by grouping.  I know. I made it harder than it really is. But even when you make a problem harder than it really is, sometimes you can come up with something interesting. In this case, I looked at your expression and rewrote it splitting the middle term into two pieces* like this:

x⁴ - 3x² + 2
x⁴ - x² - 2x² + 2
(x⁴ - x²) - (2x² - 2)
x²(x² - 1) - 2(x² - 1)
(x² - 2)(x² - 1)
(x² - 2)(x - 1)(x + 1)

And I got the same answer, even though I took a silly, round-about method.

Hope all of this was helpful - or at least interesting!

* And if you're wondering, "Why in the world did you split it in that particular way?" The answer is, "I don't really know. I just had a gut feeling it would be helpful."

"Sir , I saw your post about how to convert from alphabet to binary , in which I agree about the post. But there was a question I saw I'm my textbook which state that convert the hexadecimal number 4B3.3 to decimal. In your post here https://www.theproblemsite.com/ask/2016/01/converting-letters-to-binary, I notice that A= 65 and B =66. then I equate 66 to represent B. but after solving it there answer is different from mine .they got 1203.1875, and I got 18019.1875. How come sir? But I notice they equate there B = 11. Sir, I need your highlight on it. Thanks for talking time to read it, waiting for ur reply."

Hi Abolade, Thanks for asking this question. To understand the answer to that, I need to talk for just a moment about graphemes. A grapheme, according to one dictionary, is "The smallest meaningful contrastive unit in a writing system." That's a fancy way of saying that a grapheme is a symbol that represents something meaningful in a writing system. For example, "7" is a grapheme for the number seven. It's a symbol, and whenever you see it, you automatically know that it represents this many things:

X  X  X  X  X  X  X.

On the other hand, "72" is not a grapheme because it's not the smallest graphical unit. "72" is actually two graphemes: the grapheme for the number seven, and the grapheme for the number two.

Graphemes are also used to represent letters. "A" is the grapheme we use to represent the first vowel in the alphabet, "B" is the grapheme we use to represent the first consonant, and so forth. Of course, the graphemes for these letters might look different if you were writing a different language, such as Greek:  α β γ δ ε...

So here is where things get confusing. In base ten (our normal counting system), we have ten digits. And therefore, we have ten graphemes: 0 1 2 3 4 5 6 7 8 9. Perfect! We have just enough numerical graphemes! And if we're in base eight (also known as "octal"), we have eight graphemes: 0 1 2 3 4 5 6 7. We have more than enough graphemes (the graphemes for eight and nine don't get used in this base). 

In fact, for any base less than ten, we have more than enough graphemes. The problem is when we start talking about bases greater than ten. Then we don't have enough graphemes!

So instead of inventing new graphemes to represent these digits, mathematicians said, "Why waste the effort developing new symbols, when we've got all these other graphemes lying around not being used?" Specifically, we're talking about the alphabet graphemes. So if you are in base eleven, your graphemes are: 0 1 2 3 4 5 6 7 8 9 A, where A is the grapheme for the number ten.

Similarly, if you are in base sixteen (also known as "hexadecimal"), you have sixteen graphemes, and six of them are stolen from the alphabet: 0 1 2 3 4 5 6 7 8 9 A B C D E F.

It's very important to note that in this context, A, B, C, D, E, and F, even though they look like the graphemes for LETTERS, have a very different meaning; they are now graphemes for NUMBERS! 

A is the grapheme for the number ten
B is the grapheme for the number eleven
C is the grapheme for the number twelve
D is the grapheme for the number thirteen
E is the grapheme for the number fourteen
F is the grapheme for the number fifteen

The mathematicians very selfishly pirated letters from the alphabet to take on a completely different meaning. I mean, why not? It's not like there would be any confusion, right? Shakespeare was never going to write a sonnet about the hexadecimal number system, so there's no chance there would ever have an overlap of meaning where we were unsure whether A represents a number or a letter, right?

Wrong! Welcome to the world of computers! In a computer system, even though you can type graphemes and a computer can display graphemes, the computer does not understand graphemes. Computers "think" strictly in terms of numbers, not graphemes. Which means that people who designed computers had to come up with a system of converting graphemes into numbers, so the computer would be able to handle them.

How many graphemes are there? Well, don't forget that not only are there number graphemes and letter graphemes, there are also punctuation graphemes, mathematical operation graphemes, and special symbols like the pipe character, the tilde, etc.

So somewhere along the way, someone (or a committee of someones) had to develop a conversion chart so that whenever someone typed a character on the keyboard, there was a number that corresponded to whatever they typed. For example:

33 is the number that represents the exclamation mark grapheme
34 is the number that represents the quotation mark grapheme
43 is the number that represents the addition grapheme
65 is the number that represents the upper case "A" grapheme
66 is the number that represents the upper case "B" grapheme
97 is the number that represents the lower case "a" grapheme

Uh oh...now we have a problem! The grapheme "A" is a representation for the number 10, but 65 is the computer's value for the "A" grapheme. And this is the source of the confusion. Consider the following:

BAD = a hexadecimal number
BAD = of poor quality or low standard

Both of these statements are true. BAD is a hexadecimal number, but it's also a word! In one case, B, A, and D are graphemes for numbers, and in the other case, they are graphemes for letters! If you wanted to convert BAD (the number) into base ten, you would do this: 11 x 16² + 10 x 16 + 4 = 2980. But if you wanted to convert BAD (the text) into numbers, so the computer could deal with it, you would do this: B = 66, A = 65, D = 68.

So if you're dealing with numbers (as in your textbook), A = 10, B = 11, etc. If you're dealing with text (words), A = 65, B = 66, etc.

If only those lazy mathematicians had invented their own graphemes instead of just stealing from the alphabet, we wouldn't have this confusion!

Thanks for asking, and I hope there was something helpful to you in this lengthy explanation!

Professor Puzzler