Here's a common question among math teachers and students (and math dabblers who just like to raise people's hackles!):

"If you see 3/2x, how do you interpret it? Is it 3 divided by 2x? Or 3 divided by 2, times x? Order of operations says we do division and multiplication left-to-right, which leads to the second answer. However, if you look at the slash as a division symbol, it appears to be the other way: 3 is the numerator and 2x is the denominator."

The correct answer to this question is: it's neither.

That's right. It's neither 3/(2x) nor 3/2 times x.

So no matter which way you were arguing, you're wrong. Let me explain.

Whenever you come across something like this: 3/2, the standard reading is not "three divided by two." You read it as "three over two," (this is considered to be the proper designation for the slash symbol when used in this context). This lends credence to the notion that the slash is being used as a fraction bar, and therefore, our example should be read as a fraction: 3/(2x).

But did you know that there are specific rules for how you write fractions using standard typographic practices? First, you are expected to use a specific slash symbol, which is not your standard "forward slash" on your keyboard - it's a unicode symbol called "fraction slash." The fraction slash is designed with minimal kerning (space between characters), and there's a very good reason for this.

There's another typographical practice we must follow: we superscript the numerator and subscript the denominator. The superscripts and subscripts, combined with the minimal kerning, result in the numerator being above the slash, and the denominator below.

Thus, we would either write: ³/_2x or ³/₂x, and now you can see that proper typographic practices makes it clear which way we intended it to be interpreted.

In other words, 3/2x is actually just a typographical error, and not a real mathematical expression. It's the result of someone being lazy. (Don't worry, I've done it too!). With the sophisticated word processors we have these days, with powerful equation editors, there's no longer any excuse for any mathematician to type 3/2x. In fact, with equation editors, you can get expressions that appear much nicer than the ones that you create with superscripts and subscripts.

Of course, there is one place where this typographical error still shows up: calculators.

Many calculators are not designed for proper typographical display of fractions. So what do we do? We do one of the following:

1. Figure out which way your particular calculator handles this expression, and always do it that way.
2. The safer approach: When dealing with a calculator, always clarify your meaning by including parentheses.

Once you've settled on one of these practices, it's time to accept the fact that you haven't been arguing about some standard of mathematics, but about typography.  It's now time to do some real math, and leave behind the arguments about typographical quirks!

Professor Puzzler

Sixth grader Elise asks, "I don't get BODMAS. Can you help me?"

Well, Elise, this is one of my favorite questions, and I get asked this a lot. But I've never written it up on the "Ask Professor Puzzler" blog, so here we go!

Before I get started explaining BODMAS, I need to mention that in different parts of the world, this "rule" is known by different names. You call it BODMAS, but some people call it PEMDAS. So when I explain what it means, in parentheses I'll explain what it means to people who call it something different.

The six letters each stand for something you can do to combine numbers in mathematics:

B = Brackets (P = Parentheses)
O = Order (E = Exponents)
D = Division
M = Multiplication
A = Addition
S = Subtraction

These six letters indicate the order in which you do the operations in a mathematical expression. For example, if you see the following:

2 - (3 + 2),

You notice that "3 + 2" is in brackets (parentheses), so you do that FIRST: 3 + 2 = 5

Now you have 

2 - 5 = -3

Why does it matter which order you do things? It matters because you would get a different answer if you did the subtraction first:

2 - 3 = -1

-1 + 2 = 1

Uh oh! One way we get -3, and the other way we get 1!

Here's another example. Suppose you have 1 + 2^3 (1 + 2 cubed). If you did that from left to right, you would add 1 + 2 and get 3. Then you would cube that and get 27.

But what you're SUPPOSED to do, is evaluate the exponent first: 2 cubed is 8. Then you add 1 + 8, and get 9. It all depends on what order you do things, so you have to get the order right!

You see, we have to have an order of operations, or nobody would ever calculate expressions the same way. Order of Operations is a rule that helps to make sure EVERYONE evaluates the same expression in exactly the same way.  If we didn't have order of operations, people would get different answers for the same problem, and that would be horrible - nothing would ever get done, and none of our technology would work right because teams of engineers would always be fighting over how to evaluate the equations and formulas they work with, and if they didn't use proper order of operations, not only would things not work right, you could end up with some pretty horrible catastrophes (imagine engineers using heat formulas in nuclear reactors or power plants, and not calculating correctly how much cooling they need!).

Now here's the tricky part (and I've even had emails from MATH TEACHERS who don't understand this part!): you DON'T do all your multiplication before all your division, and you DON'T do all your addition before all your subtraction. Multiplication and division are on the same order of priority, and addition and subtraction are on the same order of priority. If a problem has both multiplication and division operations, you do them from left to right. If a problem has both addition and subtraction, you do them from left to right as well.

So really, it should be written BO (DM) (AS)* to remind you that division and multiplication go together, and addition and subtraction go together.

* Or PE (MD) (AS)

If you want some practice using BODMAS (PEMDAS), you can try our One To Ten Game, which challenges you to put toghether expressions that add up to all the numbers from one to ten.

Mathi, from Vellore, wants to know how to figure out the following game show probability:

"On a game show, a contestant is given three keys, each of which opens exactly one of three identical boxes. The first box contains $1, the second $100, and the third $1,000. The boxes are randomly lined up and the contestant gets to assign each key to one of the boxes. The contestant wins the amount of money contained in each box that is opened by the key he assigns to it. What is the probability that a contestant will win more than $1,000?"

I'm not going to answer that exact question, because I think we can make it more challenging and interesting by changing the numbers a bit. Let's do this one instead:

"On a game show, a contestant is given four keys, each of which opens exactly one of four identical boxes. The first box contains $250, the second $500, the third $750, and the fourth $1,000. The boxes are randomly lined up and the contestant gets to assign each key to one of the boxes. The contestant wins the amount of money contained in each box that is opened by the key he assigns to it. What is the probability that a contestant will win more than $1,000?"

First, we need to figure out how many ways the keys can be arranged. The first key can be assigned in 4 ways, the second one in 3 ways (since one key has already been placed), the third key in 2 ways, and then there's only one way to place the last key. That gives us a total of 4 x 3 x 2 x 1 = 24 ways. So if we can figure out how many possibilities are wins, all we need to do is divide that by 24 to get the answer.

It's a win if you place all the keys in the right position. There is one way to do that.

It's a win if you place $1000 and any one of the others correctly. (Note that you can't place $1000 and two others correctly, because if you place three of them correctly, the fourth one must be correct as well, and we've already counted that possibility!). So there are three ways to do that.

It's a win if you place the $500 and $750 correctly (but not the other two, since we've already counted that possibility!). You can do that in one way.

And there are no other combinations that work. Thus, we have a probability of (1 + 3 + 1)/24 = 5/24.

Now that we've gone through that, you'll be surprised at how easy the other problem is - there are far fewer combinations to consider!

Good luck!
Professor Puzzler

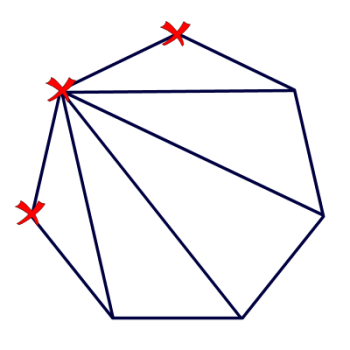
Ninth grader Michaela wants to know how you can "find the number of diagonals [in a polygon] drawn from a single vertex."

In answering this question, I'd like to point out that my diagram shows a convex polygon. If the polygon is concave, some of the diagonals will lie outside the polygon, but we would still call them diagonals.

If you look at the diagram to the right, you'll see that I've marked three vertices with an X.  Why? Because those are the vertices we can't draw a diagonal to.  You can't draw a diagonal from a vertex to itself, and you can't draw a diagonal from a vertex to its neighboring vertex. After all, drawing a line between two neighboring vertices isn't drawing a diagonal; it's drawing a side!

So, there are seven vertices in my polygon, and we can't draw diagonals to three of them, so that means we can draw diagonals to 7 - 3 = 4 vertices.

Can we generalize that? Of course! No matter how many sides the polygon has, there will always be 3 vertices you can't draw a diagonal to.

So if it has n vertices? You can draw n - 3 diagonals from any vertex.

As an added bonus (this goes beyond what you asked, Michaela!), this is how we get the formula for the number of diagonals in a polygon.

There are n vertices, and we can draw n - 3 diagonals from each one, making a total of n(n - 3) diagonals. Except...wait a minute! We've counted each diagonal TWICE (because we counted both endpoints!). So we need to divide that by two:

Total diagonals = n(n - 3)/2.

Enjoy your polygons!
Professor Puzzler

Karylle from Marinduque wants to know how you can find the ratio in an infinite geometric series, if you know that the sum is a particular multiple of the first term.

This is in that interesting class of problems in which you feel like you don't have enough information to solve it. After all, there are a lot of unknowns (the first term, the ratio, and the sum) and you'll only have one equation to work with. Whenever my students have problems like this, I tell them to simplify the equation as much as possible, and see what happens!

So let's take an example.  Let's say that you know the sum of the infinite series is 5 times the first term. Can you find the common ratio?

Well, the sum of the series is a/(1 - r), and that is 5a.

a/(1 - r) - 5a = 0

Ah...I see what's going to happen already - the a is going to factor out:

a(1/(1 - r) - 5) = 0

so either a = 0 (in which case, r could be anything, right? It's a really boring series, with all the terms equal to zero, but hey, it works!) or 1/(1 - r) = 5. This leads to:

5 - 5r = 1

5r = 4

r = 4/5

I would be inclined to say that the problem should be reworded to state that the first term is not 0, in order to avoid having "r can be any real number" as the answer. If you add in that proviso, then the answer is r = 4/5.

Hope that helps, Karylle!

Professor Puzzler