Jana from the Philippines wants to know, if you know the second and fourth terms, how do you find the first term?

Well Jana, that's a bit of a trick question, because if you don't tell me what KIND of sequence it is, I can't figure out the first term (or any other terms for that matter!). The most common types of sequences you might be talking about are: arithmetic and geometric. Of course, that's not all the possiblities. It could be a Fibonacci sequence, for example, or even a random list of numbers. Of course, if the sequence is random, there's really no way we can figure out any terms, is there?

So let's suppose the sequence is either arithmetic or geometric. And let's use the same numbers for both types of sequences.  We'll say that the first term is 12, and the fourth term is 48.

Arithmetic

The nth term of an arithmetic sequence is given by a+(n-1)d, where a is the first term, and d is the common difference.

Thus, 12 = a + d, and 48 = a + 3d.  This is a system of two equations in two unknowns, and if we solve it, we find that d = 18, and therefore, a = -6. That's our first term.

Geometric

Then nth term of a geometric sequence is given by ar^(n -1). Thus, 12 = ar, and 48 = ar^3.  If we divide the second equation by the first one (which we can only do if a and r are not zero!) we obtain 4  = r^2, from which r is either 2 or -2.  Thus, the first term is 6 or -6.

Just for Kicks

A Fibonacci sequence is a sequence in which each term is the sum of the two previous terms. So if this was a Fibonacci sequence, the third term would have to be 36, since 12 + 36 = 48.  And this leads to the first term being 24, since 24 + 12 = 36.

There you go! How to find the first term, given the 2nd and 4th terms, for three types of sequences. 

Good luck!
Professor Puzzler

Today's question is a probability question from Sue.  Her question is about how to calculate the probability of winning a game at least a certain number of times.

Let's say the probability of Sue winning Fraction Concentration against the computer is 3/4.  If she plays 8 times, how do you calculate the probability that she'll win at least 6 times?

If she wins at least  six times, that means she could win 6, 7, or 8 times.

So we're going to have to work out the probability that she wins exactly 6 times, the probability that she'll win exactly 7 times, and the probability that she'll win exactly 8 times.  Once we've found those three probabilities, we add them together to get the total probability.

Note that in the equations below, 3/4 is the probability of a win, and 1/4 is the probability of a loss (since 1 - 3/4 = 1/4).

Six wins: (3/4)^6 x (1/4)^2

Seven wins: (3/4)^7 x (1/4)

Eight wins: (3/4)^8

Now, depending on who your teacher is, and whether or not they like to torture you with fractions, you'll either have an ugly fraction, or a decimal answer.  I came up with approximately 0.1446.

Now that you know the process, you can fill in any numbers you like. Make the probiblity of winning 0.05.  Make the number of games 20. Whatever you like.

Helpful tip: Suppose you played 20 games, and wanted the probability of winning at least 5.  Using this method, you'd have to find the probability of winning 5, 6, 7, 8,...18, 19, or 20 games. Not pretty.

So instead, Find the probability of LOSING no more than 4.  That's a much easier probability, and it comes out to the same thing!

Happy computing!
Professor Puzzler

Dear Professor Puzzler,

Can you explain to me the difference between correlation and causation?  Is there a difference?

Thanks,
Martin

Hi Martin,

Correlation is a strong link between two sets of data.  For example, suppose I created a graph of electricity usage by month from January to December, and then, on top of that graph, I superimposed another graph of ice cream consumption per person by month, you might find a correlation between the two sets of data.  As ice cream consumption increases, so does electricity usage.  Similiarly, as ice cream consumption decreases, electricity usage does also.  We say there is a correlation or link, between those two data sets.  We haven't made any claims about the reason for that link; we have simply acknowledged that the link exists.

Causation is a word that is used to indicate that one thing causes another.  Causation is NOT the same as correlation.  Consider the example of the ice cream and the energy usage.  Does eating ice cream cause you to use more electricity?  Of course not!  Does using electricty cause you to eat ice cream?  No!  Those are both silly ideas!

So what's going on here?  It's simple: as temperatures increase, people are more eager to eat ice cream, because it cools them down.  But at the same time, people are running air conditioners more, and their refrigerators are working harder because of the heat.  Both the ice cream consumption and the energy consumption are a result of the changing temperatures from one month to the next.

This is why it's very important to understand that correlation does not imply causation.  Just because two things have a correlation does not mean that one causes the other!

Here's another example.  Take a look at the chart below.  It's used as proof that autism is caused by the use of herbicides on crops:

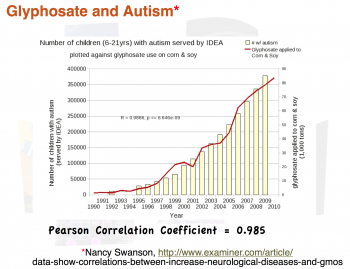
It shows a very definite correlation between herbicide use and autism.  Later on we'll tear this graph apart, because it is one of the most attrociously unscientific graphs I've ever seen, and the fact that it's linked from the home page of an MIT researcher is downright embarrassing.  But we'll get to that a bit later.

Now that you've looked at this graph and drawn the obvious conclusion: Herbicide causes autism, take a look at the next graph, which shows another, quite surprising correlation.

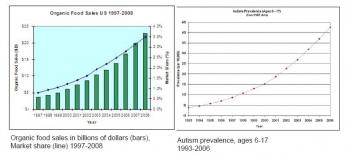
Yes, that's right - you're reading that graph correctly.  There is a very clear correlation between purchase of organic foods and autism.  The conclusion is very clear: Organic foods cause autism!

I'm sorry, you can't have it both ways.  If the first graph (which is merely a correlation) is proof of causation, than so is the second one.

The real challenge is this: if you can't eat chemically treated crops, and you can't eat organic crops, how do you avoid autism without starving to death?

The Embarassing Glyphosate and Autism Graph

I promised we'd tear apart that herbicide/autism graph, and we will.  This graph has been shared on the home page of an MIT researcher (whose post graduate degrees are in Electrical Engineering and Computer Science).  Never mind the fact that she probably doesn't have any business meddling in biology related stuff, if you have a masters degree or a Ph.D. in any subject area, you know enough to realize that this chart is horrifically nonsensical.  For crying out loud, my high school science students probably know enough to realize how dumb this chart is.  

So, is this graph really so bad?  And if so, how?  Oh, let me count the ways...

1. The graph uses total numbers of autism cases instead of autism cases per capita, which means it does not take into account population increase (which was significant between 1990 and 2010).
2. The graph shows only autistic children served by IDEA (Individuals with Disabilities Education Act).  What's wrong with that?  Oh, I don't know, maybe the fact that IDEA started serving autistic children in 1990, which means the first few years of that graph are ramped up because IDEA was ramping up.
3. The graph does not take into account the fact that diagnosis rates have significantly increased over that time interval; more and more children who used to be diagnosed with mental retardation are now being diagnosed as autism spectrum.
4. The graph shows total gallons of herbicide, without any reference to gallons per acre, or number of acres of cultivated land.
5. One chart represents USA numbers (autistic children served by IDEA) while the other chart is worldwide (do you really think we don't export significant amounts of corn and soy?  Check the USDA site if you doubt it!)  If you're comparing US numbers with global numbers, you're not just comparing apples with oranges, you're comparing apples with harmonicas.  Or some equally absurd comparison.
6. The correlation goes even further out the window if you attempt to limit your gallons of herbicide to ONLY crops used for human consumption.  Based on a quick scan of USDA and NCGA websites, it appears that the amount of corn used for ethanol is from 20% to 40% of the entire corn harvest, and that number is rapidly increasing.

Are there more problems with this graph?  Oh, undoubtedly!  Those are just the ones I came up with off the top of my head, without doing any serious research.  And yet, ironically, the "researcher" who shares this on her home page has the audacity to whine about scientific journals that have unfair standards of statistical analysis.

So, Martin, you probably got more than you bargained for - this turned into a little rant (hope you don't mind).  But I hope it'll help you remember that just because two things have a correlation doesn't mean that one caused the other!

Professor Puzzler

P.S. If you're wondering why I didn't rip the second chart to shreds, it's because no one actually believes the second one; it was created entirely to prove a point. The organic-food chart (along with a diabetes chart) can be found here.

Question

Hi Professor Puzzler, I was wondering if you could explain what an axiom is?

Katie M, Grade 11
South Dakota

Answer

Hi Katie,

Well, I'm guessing that you're taking a Geometry class, because that's when many students first see that term.

An axiom is something that you believe or accept to be true without having ever proven it.  It is something that you consider to be "obviously true." You might not realize it, but your life is filled with axioms - things that have never been proven to you, but you believe anyway.  I once asked a group of high school students to name some things they couldn't prove, but they were confident of anyway.  Here were some of their answers:

• My parents love me.
• The sun will rise tomorrow.
• Gravity keeps me from falling out into space.
• There is a God.
• 1 + 1 = 2.

Why are axioms important? Because when you are proving something, there will always be fundamental building blocks of ideas that your proof is based on, and it's important to remember that the most fundamental building blocks are actually things you haven't proved at all.

In a way, an axiom is sort of like what the Bible says about faith: faith is the substance of things unseen.

Euclid had some axioms (or postulates), and one of his very important axioms was that if you have a line, and a point that's not on the line, there's only one line that goes through the point, and is parallel to the line.  That might seem obvious, but some other mathemeticians like Lobachevsky, Riemman, and Gauss had some different ideas, and their notions of geometry turned out to be very different from Euclid's.

The assumptions you start with can drastically change your results!

In modern usage, the "obviously true" concept is not how axioms are always viewed; in another sense, we could view an axiom as simply a "rule of the game" in mathematics.  In other words, mathematicians might say, "Let's start from assumption X, and see what sort of mathematics we develop!"  The assumption, or axiom they begin with may not be something that's "obviously true," but often valuable results come from such game playing.

Thanks for writing,
Professor Puzzler

We have a new math 6th grade series where Order of Operations has changed and PEMDAS is no longer the standard. Have you encountered this yet? We have Glenco, 6th grade. Multiplication and division still come before addition and substranction, however, now it works left to right whereas before it was multiplication before division.

In some areas of the world they use a different acronym (such as BODMAS or BEDMAS), but these are still the same thing as PEMDAS (Please Excuse My Dear Aunt Sally).

Believe it or not, the PEMDAS order of operations is not only still correct, but it's always been what you just described.

The acronym PEMDAS can be deceptive, if it’s not taught correctly.  How it should be taught is:

P: Parenthesis first
E: Exponents next
MD: Multiplication and Division next
AS: Addition and Subtraction last

Notice that the M and D are grouped together, as are the A and S.  This is because Multiplication and Division are at the same priority level, and should be done in left to right order. Likewise, Addition and Subtraction are at the same priority level, and should be done in left to right order. 

Unfortunately, many  teachers don’t realize this, and teach that all multiplication is done before all division, and all addition is done before all subtraction.  I was taught that way all through elementary school, and it wasn’t until I hit Jr/Sr high that I found out that Multiplication and Division are at the same priority level, as are Addition and Subtraction.

If you are looking for a game that forces students to think through Order of Operations, here's a game I created several years ago: One To Ten.