Normally I just post responses to questions people ask, but we haven't had any interesting questions this week, so I thought I'd take a few minutes to answer a question that gets asked a lot (even though no one has specifically asked me!)

Here's the question: "Why is the Common Core method of doing subtraction so different from, and more complicated than, the old way of doing it?" 

The standard example that goes with this question looks like this:

There are several answers to the question, and I'm going to summarize them before going into details.

1. The method on the right is not the "Common Core way" of doing subtraction.
2. The method on the right is as old as the way on the left, and most schools have taught it for generations.
3. The people who created this example (or the video you saw) were deliberately trying to mislead you.

Not the "Common Core Way"

The algorithm students are being taught to do subtraction looks exactly like the one on the left. Students write the two numbers in a column, do subtraction by place values, doing borrowing where appropriate. It's the good old stand-by - it works, it's effective, it's mathematically sound, and it will never go away.

So what is the thing on the right, if it's not a replacement for the "old" way of doing things? 

It's ANOTHER Old Way

It's the traditional method taught for doing mental arithmetic. If you need to do a math problem without the aid of a pencil and paper (or a calculator) the method on the right, once you've learned it, is vastly superior.

Take the following example: what's 262 - 187? I was able to do this mentally, using the "common core" method, more quickly than you could write the problem down on paper. What did I do? I said, "I need to add 3 to get from 187 to 190, then another 10 to get to 200, then another 62 to get to 262, so the answer is 62 + 10 + 3 = 75. Meanwhile, you're still thinking about borrowing from the tens and the hundreds place, and trying to do it in your head.

This method is so superior (when it comes to doing mental math) that teachers have been teaching it for generations. I learned it, and when I checked with my parents, they confirmed that they had learned it as well. In fact, my mother attests to the fact that when she was a teenager, it was impossible to get a job in retail if you couldn't do that. It was necessary for making change.

I also have heard from someone that it is still required in their firm because cashiers have to be able to make change even if there's a power failure and their register system goes down!

Dishonesty In Media

I've seen so many of these images and videos purporting to prove that "The Common Core way is horrible," and they all have one thing in common. They don't use examples like 262 - 187; they all use ridiculous numbers that make the "common core way" look horrible and cumbersome, and the "old way" simple. Of course it's easier to use the "old way" when subtracting 12 from 32 mentally! Duh! There's no need to even THINK about pencil and paper for that.

But here's the thing...try randomly picking numbers and attempting to do both processes mentally. You'll discover what people in the business world have known for centuries - the method on the right is hands down the winner.

And if the method on the right is the hands-down winner* - isn't it strange that 100% of the images and videos produced make it look otherwise? If the majority of random examples show you one thing, but 100% of the propaganda you've seen shows you something else, that should tell you something...you are being deliberately misled and deceived.

Conclusions...

Are there issues with Common Core? Oh, I'm sure there probably are. But here's the thing...if you want to complain about Common Core, you need to complain about the right thing. If you complain that this method is being taught, I hate to say it, but you're probably accomplishing nothing except making your local school officials think, "Wow, this guy is some kind of nitwit..."

So figure out what the real problems with the math curriculum are. One parent told me, "My kid is too young to learn this technique." Fine! If you think that's the case, then complain about that! But THINK before you complain. Make sure your complaints are real and valid before you bother the (probably) overworked and (likely) underpaid educators who are working hard to help prepare your child for adulthood in a crazy, complicated world!

* Last summer contractors were hired to come in and dig a hole for the foundation of our new home. After they left, we were looking at the hole they dug and saying, "That hole doesn't look like it's deep enough." So we did some measuring. Of course, the depth had to be measured not from the ground, but from a pre-determined point above the level of the ground, which meant we needed to do some subtracting, and therefore (since we didn't have calculators on hand) some mental arithmetic. I discovered something I never knew before that day: the "common core way" not only works for integers and decimals, it also works when your measurements are in a combination of feet, inches and fractions of inches. I could never have calculated that difference mentally without this technique that I learned as a student. And after double-checking ourselves a couple times, we were able to call the contractor and say, "You did this wrong." He came back in with his laser level and verified that he was wrong and we were right. Do I thank "Common Core" for that? Of course not! I thank my math teachers who taught me how to do this long before Common Core was even an idea in anyone's brain.

A visitor from Orlando asks:

"example of how to set up trapezoid ABCD, ABllCD, measure of interior angles are distinct and measure of

Well, there are a couple questions in here, one about an angle, and one about how to set up the trapezoid. Here's a picture that shows the setup of the trapezoid. Note that AB and CD are parallel, as the statement of the problem shows. Also note that the letters are in order around the vertices - from A to B to C to D, since the trapezoid is called ABCD. If the trapezoid had been named ACBD, we would have needed to rearrange our vertex names to match that.

We'll come back, in just a second, to the question of how to make sure the interior angle measures are distinct (all different).

But first the question is, how do we find the measure of angle A, if we know that the measure of angle D is x. If you've studied a bit of geometry, you may know that AD is a transversal between parallel lines AB and DC, and that interior angles A and D are consecutive interior angles, which is a fancy way of saying that they're on the same side of the transversal, between the two parallel lines. And consecutive interior angles are supplementary. This means they add to 180 degrees.

Therefore, m

m

m

As for how we make sure the angles are all distinct, there are two things we need to ensure.

First, we need to make sure that none of the angles are 90 degrees, because if ONE of them is 90 degrees, then the associated consecutive interior angle must also be 90 degrees, and that means the angle measures aren't all distinct. Thus, we can't have a right trapezoid.

The other thing is, we need to make sure it's not an isosceles trapezoid (AD = BC). If it's iscoseles, then m

Therefore, if the trapezoid is neither right nor isosceles, the angles will have distinct measures.

A visitor from India poses the following question: "You have five fives. 55555 now, (i) Arrange the fives to get largest possible value (ii) arrange the fives to get a value equal to 1. (iii) Arrange the fives to get a value less than 1. (iv) Arrange the fives to get a value equal to 56. remember : do not use the signs +.-,x,/ . But a bar or line between two digits can be helpful"

If you read my previous blog post on matchstick puzzles, you know that I don't expect there to be just one solution to this, and that anyone who thinks there is just one solution is probably being naive. Furthermore, this puzzle requires you to "think outside the box," and the person who gave you this puzzle may have a specific way they expected you to think outside the box, and therefore may not like your solutions.

I have solutions for all four parts.

They're probably not the solutions the problem poser was looking for.

And I'm not going to tell you my solutions.

Instead, I'm going to give you some pointers in directions that may help you solve the puzzle. I'll suggest to you some of the ways I "thought outside the box," and let you try to work through the possibilities to arrive at your own solutions (which might be different from mine!)

I also am not going to tell you which "outside the box" idea I used for which part of the puzzle. I don't want to give you too much help!

Ready? Here we go...

• First, I'd like to point out that your problem certainly has a typo in it. There are commas separating each of the symbols you can't use, except that between the plus and the minus, there is no comma - there is a period instead. This is certainly a typo, since the list is inconsistently displayed otherwise. This is important, because there are solutions available which make use of a decimal marker, and the decimal marker has NOT been eliminated in the rules. (If they had intended to eliminate the decimal point, they should have written: "do not use the signs +,.,-,x,/" There is no way to read their actual sentence that isn't grammatically nonsensical, so we'll make the assumption that the decimal point is allowed.)
• You have hopefully thought of using exponents, but have you thought of using exponents within exponents? Or even exponents within exponents within exponents? Something like this:

• Although the forward slash (division symbol) has been eliminated from use, the horizontal fraction bar has not. In fact, the statement of the rules almost begs you to use the fraction bar.
• Speaking of bars, don't forget that a bar over a digit represents a repeating digit.
• Did you know that if you flip (not rotate) a five upside down, it's a two?
• Eliminating specific operators implies that anything not specifically eliminated is fair game.  Have you ever run across the "bracket" operator? The brackets represent the operation "greatest integer of." If you see the expression [3.53], that evaluates to 3. Basically, you just drop the stuff after the decimal.
• Following along with my previous observation, the "factorial" operator has not been eliminated either, so you could do 5! if you wanted, and 5! = 5(4)(3)(2)(1) = 120.

Using just those ideas, you can come up with solutions for all four parts of this puzzle. Of course, if you take it back to the person who posed the puzzle in the first place, they may say something like, "But you're not allowed to flip the fives upside-down," or "You can't use the greatest integer function," or "You can't use a decimal point," or have some other lame excuse why your solution isn't the "correct" one.

Ask me if I care.

Nope. I don't. Thanks for asking. If they didn't want you to do certain things, they should have specified in the rules! :)

Good luck working out the rest of the puzzle. If you figure out some solutions, I'd love to hear back from you!

Professor Puzzler

The following blog post is an example problem designed to show why I don't answer peoples' "Matchstick Problems" on this blog. We've set up a new "Codes and Riddles" forum on our Community Forum, so you can share your matchstick riddles there and ask for help solving them. In order to post in the forum you must have a free membership account (click the login link at the top of the page to get started). We have an unusual "CAPTCHA" for the forum - instead of typing letters to prove you're human, we require you to solve at least 5 puzzles on the site before you post anything. (Here's a hint: Blackberry Game is about the simplest game on the site, so you can rack up your 5 games easily there!)

You wouldn't believe the number of times people have contacted me to ask me to solve a matchstick problem for them. You know the kind of problem I'm talking about, right? You're given a layout of matchsticks, and you are asked to move two (or one, or three, etc) matchsticks to form the largest number possible.

Here's an example: move 4 matchsticks to make the largest number possible out of the following:

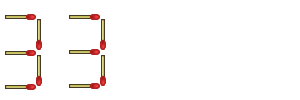
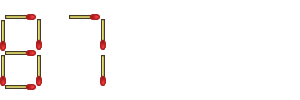
And to this second complaint, I reply, "Of course I moved four! I picked up two others and set them back down again!"

"That's not allowed," you say.

"Fine," I reply. "I didn't just set them down; I swapped them."

Here's a better solution, which, in a literal sense, thinks outside the box - instead of limiting myself to the two digits given, I expand the number to the right. This is a fairly obvious solution, and you shouldn't have any complaints about it:

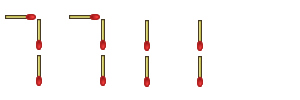
"There," I say, "that's about 500 quintillion - beat that!"

"You cheated! I never said you could use exponents!"

"And you never said I couldn't," I reply.

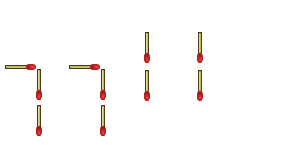
But wait! Who says a number one has to be two toothpicks tall?  Aren't they still ones if they're made out of one matchstick apiece? Couldn't we do this:

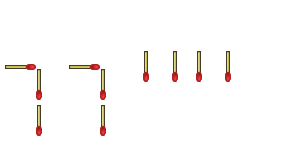
"Cheater!" someone declares, "You can't change the structure of the numbers!"

"I haven't changed the structure." I reply. "Exponents are supposed to be smaller, so I've formatted it perfectly."

Are we done yet? Are there more ways of thinking outside the box? Sure! Take a look at this one:

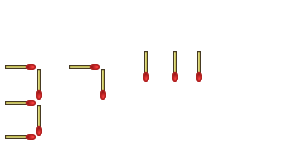
"Yeah, but you knew it was a seven, didn't you?"

"Besides," you protest, "you only moved three matchsticks - you couldn't have swapped two others, because that would have meant moving FIVE matchsticks"

"Ah," I say, glad to have you distracted from my malformed seven, "I picked up one that I wanted to move, and one that I didn't want to move, placed the one I wanted to move to the position of the one I didn't want to move, and then moved that one to the new position."

"Okay, fine!" you say, "You win!"

So what is that number? Well, we need to evaluate 7¹¹¹ first, and that's 3.9e93, and when you try to raise 3 to that number, you're going to get an overflow error on your calculator.

And so I sit here smugly satisfied with myself - until someone else comes along and says, "Wait a minute! If you're going to let him get away with that malformed 7, then I can do this:"

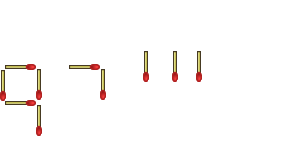
No! Even though I've come up with solutions that are too big to run through your calculator, this is just what I came up with on the spur of the moment - there are almost certainly better solutions out there! *

So what's the point? The point is twofold:

1. Have fun with these kinds of problems, but if someone asks you one of these and doesn't clarify the rules of what you can and can't do, just have fun thinking outside the box, and when they say, "You can't do that!" enjoy the opportunity to annoy them with the response, "You never told me I couldn't!"
2. If you ask me to solve your matchstick puzzle, I will simply direct you to this blog post, because I would almost certainly NOT come up with the solution the problem poser was looking for, so why should I even try - it's not MY puzzle after all! :D

Happy Puzzling!
Professor Puzzler

* Within a half an hour of posting this, two more even better solutions popped into my head - neither of which require malformed numbers.  How many can you find that beat 9^(7^111)?

Yesterday we received the following question: "What is estimating?"

This is a fairly broad question, but it's worth answering.  I'll explain briefly what it is, and then after that I'll talk about why it's important to be able to estimate.

The following is a screen shot from our game "Guess It!" in the Junior section of the site.

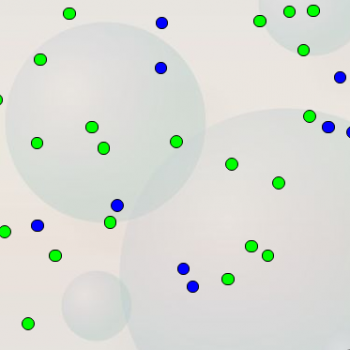
When you are playing "Guess It," the site might ask you a question like "Are there more green dots or blue dots?" You will automatically say, "There are more green than blue." But how do you know? Did you stop to count all the green dots, and then count all the blue dots? Hopefully you didn't! Hopefully you were able to quickly scan the image and recognize that there are more green, without taking the time to count them. That's estimating.

The site might ask you "Is the number of green dots closer to 10 or 50?" Do you need to actually count the green dots in order to answer the question? No!  You've probably got a good sense for what a group of ten dots would look like, and it's fairly obvious that the image doesn't contain 5 groups like that. So you would say "It's closer to 10 than 50!" That's estimating.

Estimating is when we don't need to have an exact answer; we just want to be "in the ballpark."

Why Is It Important?

Suppose you had $50.00 in your wallet, and you went grocery shopping. You don't have a calculator with you, and you don't want to add all your purchase prices by hand, but you want to be sure you don't get to the cashier with a cart full of items that add to more than $50. Your items cost $7.96, $3.20, $13.84, and $4.42. You can do some estimating like this: "I'll round all my items up to the next multiple of five so I can add them easily. If the sum is less than 50, then I know I'm okay. $10, $5, $15, $5. 10 + 5 + 15 + 5 = 35, so I'm okay!"

Estimation is also a great way of checking to see if your conclusions are reasonable. If I'm trying to calculate how long it will take an object to fall to the ground from the roof of my house (yeah, I calculate silly stuff like that, because I'm a Physics teacher!), I can mentally picture it falling, and estimate: "Well, it certainly won't take more than 5 seconds!" and so if I do my calculations and come up with an answer of 35 seconds, I know something must be wrong!

I do a lot of estimating while I'm teaching. Using the "falling to the ground" example above, I know that the acceleration due to gravity is 9.8 m/s², which is not a nice number to work with if you don't have a calculator. But it's really close to 10, so if I'm doing a freefall problem on the board, and don't want to pick up a calculator, I'll do an estimation by replacing 9.8 with 10, and work out an approximate answer in my head. Then, when my students start telling me the numbers they came up with, I'll ask myself, "Is that reasonably close to my answer?" If it is, I'll feel confident that they got the answer correct.

In general, I find that my students who are good at estimation do much better than the ones who do not, because they are quicker to recognize whether their answers even make sense! That's not just a good thing in school; it's a skill that will transfer to your job and your every-day life.