Open up a flexible tape measure, until the year of your birth (last two digits) plus 100 is showing. Now bend the tape measure over and bring back the end of it until it lines up with your birth year. Now find the last two digits of the current year, and see what corresponds to it on the other side of the loop you've created. Take the last two digits of that number and subtract it from 100 and you'll have your age. Why does this work?

First of all, let's start by setting some limitations on this, because it doesn't always work. A couple towns over from us there is a woman who just turned 106. If we try this trick for her age, we find out that she's 6 years old. So if someone is over a hundred, we have to use a little common sense and say, "Well, she doesn't look like she's 6 years old, so we'll add 100 to that."

So in exploring this, we'll ignore any age 100 or more.

Also, we need to agree that we're talking about "age at the end of this year," because if the person hasn't yet had their birthday, this trick is off by one year.

With those things clarified, here's an example. My grandmother was born in 1916, so I'm going to fold over the tape measure to look like this.

If I scan back up the tape measure until I find the current year (2015), I find that the number across from it is 101. Now I take the last two digits (01) and subtract that from 100, getting 99 (which is my grandmother's age).

Let's stop for a minute and think about what we've done. We have a total of 116 inches extended on the tape measure. What significance does that number have? 

Let's define some variables and see if we can make some sense of how that number is going to play into the tape measure game.

Since the birth year is the current year minus the age,

(100B_f + B) = (100C_f + C) - A

Let's do a little algebraic manipulation on this equation, rearranging terms until C - B is by itself.

C - B = A - 100(C_f - B_f) 

On the left side of the tape, I see the number B + 100. On the right side, I see 0. Since the left side is increasing from top to bottom, and the right is decreasing from top to bottom, every time I move up a number on the right, I'm moving down a number on the left.

Thus, if I move up to C on the right, I'm decreasing the value on the left by C, giving me: B + 100 - C.

Let's take that B + 100 - C and rearrange it:

100 - (C - B)

Since we found C - B in a previous equation, we can substitute this:

= 100 - [A - 100(C_f - B_f)]

= 100(C_f - B_f + 1) - A

Since we're only looking at the last two digits of the number, we can do a bit of modulus (remainder) math*, and say that 100(C_f - B_f + 1)  is congruent to 100 (mod 100), and therefore, what we're looking at is:

100 - A.

What happens if you subtract that from 100?

= 100 - (100 - A)

= 100 - 100 + A

= A (Current age!)

And there you have it. That's the algebra behind why this trick works.

As an added bonus, the trick also works if you just slide the tape measure out to the birth year, instead of 100 more than the birth year. BUT now we have the stipulation that it doesn't work if we haven't extended enough to get the current year on the right-hand side of the tape measure. So we could say, "Slide the tape measure out until the current year is on the right, and then keep sliding it until the last two digits on the left match the birth year." This saves you having to go out an extra 100 inches in many cases.

* This step of doing some modulus math is the reason the trick doesn't work for people over the age of 100; what we're actually finding is their age mod 100, or the remainder when their age is divided by 100. This has the effect of returning only the last two digits of their age.

Curtis asks us for an explanation for how to do a factor tree.

If a number isn't prime, then it can be written as a product of prime numbers. This product is called the "prime factorization." It's very useful to be able to find the prime factorizations of numbers, because that will help you determine things like the greatest common factor (GCF).

A factor tree is an easy way of finding the prime factorization of a number. So let's do a factor tree example. Let's say we want to find the prime factorization of the number 1,260. First, we ask ourselves, "Is there a pair of numbers that multiply together to make 1,260?"

That question has a lot of answers: 1,260 is 2 x 630, it's 3 x 420, it's 5 x 252, etc. When I did this, the first pair of numbers I spotted was 10 and 126. After all, if a number ends in a zero, like 1,260 does, we know it has to be a multiple of 10. So I drew a pair of arrows coming out of 1,260, and wrote 10 and 126 under the two arrows like this:

I could have picked any of those other pairs, and it also would have worked fine.

Now that I've done this, I need to ask myself, "What is a pair of numbers that multiplies to 10?" and "What is a pair of numbers that multiplies to 126?"

For ten, I came up with two and five, so I drew arrows coming out of 10, and wrote two and five under them.

For 126, I came up with 7 and 18, so I drew arrows coming out of 126, and wrote 7 and 18 under them.

As I'm writing these, I realize that 2, 5, and 7 are all prime numbers (they can't be split up any more) so I draw circles around them.

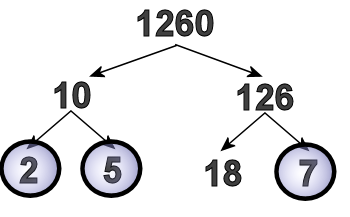
Some teachers, instead of having you circle the primes, will say, "Draw one arrow straight down from the two, and write two under it, so you keep bringing that two down to the bottom." Either way, you need to make sure you don't lose track of those prime branches!

Eighteen can split into factors; I chose to do 2 and 9. (I could have done 3 and 6 instead). So now it looks like this:

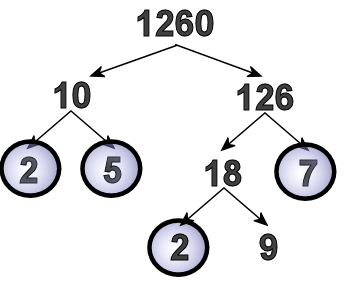
We're almost done, because we've just got one number to split up (2 is prime, so we circle it, and then we just have to deal with the 9.) 

Nine is three times three, so we make our arrows, and write two threes.

Since the threes are also prime, we'll circle those, and our prime factorization looks like this:

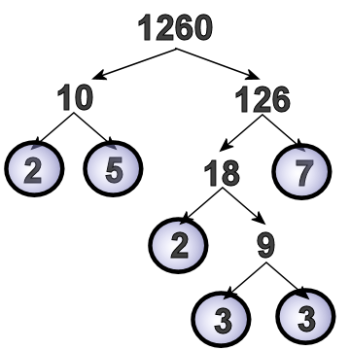
Now that we've split 1,260 up into prime factors, we can say that 1,260 = 2 x 5 x 2 x 3 x 3 x 7.

But it would be better to write each prime factor only once, using exponents: 1,260 = 2² x 3² x 5 x 7.

Hope that's helpful!

Professor Puzzler

Eighth grader Sandesh asks, "consider y=x*x*x*x*x*...... up to infinity . hence y=x*y which means either y=0 or x=1 how can we explain it?"

First, you need to understand that what you're talking about is called a LIMIT. We can't actually multiply x times itself an infinite number of times, because there isn't enough time in the universe to do that!

What we can say is that we're going to multiply x by itself n times, and n is a really really big number. In fact, we say that n is "approaching infinity."

Now, some things have limits, and some things don't. For example, consider this:

1/2 x 1/2 x 1/2 x ...

If we multiply 1/2 times itself a billion times, we get something really close to 0, and if we multiply it a billion and one times, we get something that's even closer to zero! And if we keep multiplying, we get closer and closer to 0. So we say the LIMIT is 0, or that it converges to zero.

On the other hand, consider this:

2 x 2 x 2 x 2 x ...

If we multiply 2 times itself a billion times, we get an astronomically huge number. But if we multiply it a billion and one times, we aren't getting closer to any particular number, we're just getting even more astronomically huge. So this doesn't really have a limit. We say it diverges.

So, I think the important thing you're missing here is that x * x * x * x ... is only convergent for certain values. it converges if x is between 0 and 1 (inclusive). Otherwise it is divergent. (It's divergent for x < 0 because the product keeps flopping back and forth between negative and positive each time you multiply, so it never settles in on any one value. It's divergent for x > 1 because the product explodes to astronomically large values).

And if it's DIVERGENT, then you aren't allowed to do your cute little substitution. However, if the expression does converge (x is between 0 and 1) then your substitution is a useful way of looking at it. (There are more precise ways of looking at it, that you'll learn someday when you take a calculus class, but this will be sufficient for now).

Here's why your substitution won't work in all cases:

The original equation is: y = xⁿ, where n is approaching infinity.

Rewrite it slightly: y = x * x^{n - 1}

x^{n - 1} is the part you want to replace with y.

You see, what you're really doing when you substitute is, you've assumed that "the limit as n approaches infinity of x^{n - 1}" is the same as "the limit as n approaches infinity of xⁿ". But this is only true if xⁿhas a limit! When xⁿ has a limit, then you can do your substitution:

y =xy.

y - xy = 0
y( 1 - x) = 0
y = 0 or x = 1

And this is actually the correct result, for the situation when xⁿ has a limit. Because if xⁿ has a limit, x must be between 0 and 1. If x is any number LESS than 1, then when you multiply it by itself a billion times, you get something really close to zero. We say that its limit is 0. And if x = 1, then y = 1 as well, both of which fit your solution.

The entire study of limits is much more complex than I've made it seem here; I've done my best to keep the math and the terminology fairly simple (hopefully I've succeeded in that!). When you get into a Calculus or Pre-Calculus class, you'll find that there's a lot more to it, but hopefully that'll at least whet your appetite for more!

Professor Puzzler

Erin shared the following image, and wants to know if this works. (Click on the image to see a larger version).

Well, Erin, there are really two questions here, and I'm going to try to answer both of them. The first question is the one you asked - Does it work? The second question is one you didn't ask - Is it practical?

Does it Work?

When you ask if it works, I assume you really mean, "Does it work all the time? Or just for this specific example?"

The answer to that is, yes, it always works. I can show you some simple algebra to help you see that this always works.

Suppose you have the equation A - B = C (In this case, A = 5000, B = 2384, and C = 2616)

If we subtract 1 from the number we start with, and the number we're subtracting from, we get:

(A - 1) - (B - 1). If we distribute that negative in front of (B - 1), we get an equivalent expression: A - 1 - B + 1. But the -1 and the +1 are like terms which can be combined, to give A - B, which is still C. So yes, this always works.

What's more, an altered version of this process works with addition:

Suppose you wanted to add 9999 + 4352. Add one to 9999 to get 10000 and subtract one from 4352 to get 4351. Now do 10000 + 4351, and you have 14351.

Is It Practical?

If you are trying to do the problem mentally, then yes, I would say this is practical. However, if you're trying to do it on paper, you should consider that it actually takes more writing to write the entire problem over again, instead of making the few marks required to indicate where you've borrowed. Of course, if you don't understand regrouping/borrowing, then the method shown here will be very appealing to you, even if it takes more writing.

I was trying to think of a real world application where this would be useful, and it didn't take much thought. Suppose I'm at the store, and I have a ten dollar bill. I want to buy an item that costs $3.54. What will my change be?

Instead of mentally trying to do $10.00 - $3.54, I can mentally do $9.99 - $3.53 = $6.46.

Not bad.

You've seen the videos, you've probably shared them on Facebook or other social media...the videos that tell you, "This is how the Japanese multiply numbers!"

Except...do they really?

First, here's an example: 

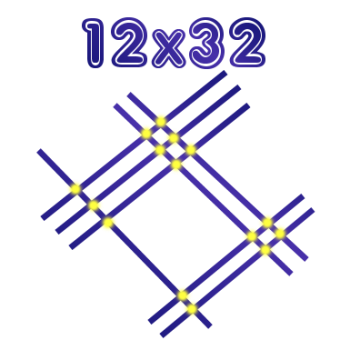
The question is, how do you multiply 12 x 32 the Japanese way?

Well, supposedly, the Japanese solve this by drawing one line diagonally from the left down to the right, followed by a pair of lines going in the same direction. The one line, followed by the two lines, represents the number 12.

Similarly, three lines are drawn together from the left up to the right, followed by two more lines from the left up to the right; these sets of lines (3 and 2) represent the number 32.

Now you draw a circle around every intersection point, starting over on the right. There are 4 intersection points. That means that the last digit is 4. In the middle there are six intersection points (at the top) and two more at the bottom, making a total of 8. Thus, the middle digit is 8. Finally, there are 3 intersection points on the left, so the first digit is 3.

Therefore, the answer is 384.

I'll give you a second to use your old algorithm (or your calculator!) to verify that this is correct.

Does this always work?  Well, yes...and no.

The videos that display this process rarely show what happens if the sum of your intersection points is greater than 10. If that happens (which, really, why wouldn't it?) your process is a bit more cumbersome, and you have to transport a group of ten dots as a single dot in the next place value. In other words, you have to carry.

That's not a big deal, though; you already have to carry with your algorithm. So what's the problem with this algorithm? Well, the people who make these videos are very careful to make sure they do multiplications with small digits. You'll see things like 12 x 32, or 113 x 21, but you'll never see one of these videos with 978 x 88.

Why not? Gee...I don't know...why don't you try drawing the diagram for that problem, and see what it looks like. While you're busy drawing that diagram, I'll solve about five more multiplication problems. You'll need to draw forty lines, circle and count 201 intersection points, and meanwhile, I've moved on to my division lesson, because I got tired of waiting for you.

Do the Japanese do this when they're multiplying? Of COURSE NOT! I don't know if any Japanese teachers actually show this to their students (read comments on videos and you'll find people saying things like, "I taught math in Japan for 25 years and never saw this.") but if they do show it to their students, it's only as a way of visualizing place value in a different way; nobody actually expects their students to use this as their go-to multiplication algorithm.

And yet, wherever you see videos like this, you'll see comments from parents saying things like, "If I had learned it this way, I wouldn't have ever had problem with math," or "I'm going to meet with my kid's teacher and ask why in the world she's not teaching it this way!"

Oh dear! Please give your child's teacher a break! Let them teach math, and don't force them to spend an afternoon explaining to you why the latest craze to hit the internet isn't actually even slightly useful as a multiplication algorithm.

And if you got fooled by the "Japanese Multiplication" video, odds are good you also got fooled by the "Oh noes! Have you seen how Common Core does subtraction????" videos, so you'll want to read our post about "Common Core" Subtraction.