Bianca, an 11th grader from Canada asks, "Hello, I need help in math, how can I prove that the cosine of 36 is equal to the number of gold divided by 2."

That's a great question, Bianca. For anyone who doesn't know, the "number of gold" or "the golden ratio" is the number (1 + SQR(5))/2, which is approximately 1.6180339887. This number is interesting largely because the Greeks were fascinated by it, and because certain sequences which appear in nature sort of "zero in" on this number.

So how do we prove that the cosine of 36 degrees is this magical number? Well, we'll start by drawing a picture of an isosceles triangle which has angles 36-72-72.

Let's add a line segment to this triangle; let's add an angle bisector from angle B to the opposite side.

This produces some interesting similarities and congruences. For starters, measure of angle DBC is half of the measure of angle ABC, or 36º. Since the measure of angle DCB is 72º, we have triangle ABC similar to triangle BDC, and BC = BD (because the triangle is isosceles).

We can use some similar reasoning on triangle ABD to conclude that it is also an isosceles triangle, with BD = DA.

Putting all of this together leads to BC = BD = DA.

Now, since triangle ABD is similar to triangle BCD, we can conclude that

AC / BC = BC / CD

BC² = (AC)(CD)

Now we can do a substitution, by noting that AC = AD + DC which equals BC + DC.

BC² = (BC + DC)(DC)

BC² = (BC)(DC) + DC².

At this point, I'd like to do two things to this equation. First, I'd like to divide both sides by DC², and then I'd like to do a substitution: x = BC/DC. This results in the following equation:

x² - x - 1 = 0.

This can be solved using the quadratic formula: x = (1 + SQR(5))/2, or the golden ratio!

But how do we get here from to the trig function you want? Well, for starters, since the larger triangle is similar to the smaller one, we also have AB/BC = the golden ratio.

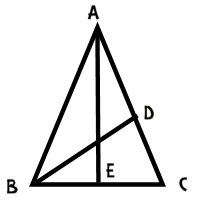
Now if we draw a perpendicular down the middle of the diagram, we've got AB/BE = 1/2 of AB/BC, or half of the golden ratio. This means that BE/AB is 1/2 of the golden ratio. But BE/AB is the cosine of 72 degrees, since AEB is a right triangle.

Thus, cos(72º) = 2/x, where x is the golden ratio.

From here we can use a half angle identity:

cos(36º) = SQR((1 + cos(72º))/2)

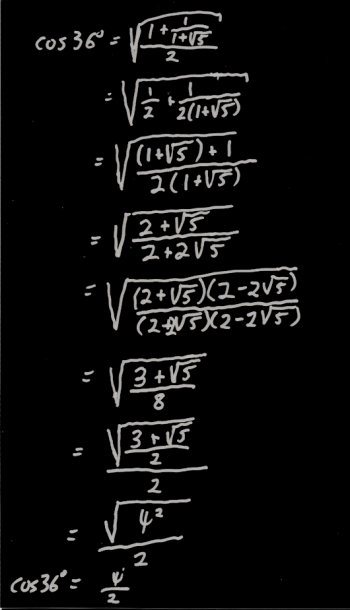
Now if you think that looks ugly, you're right. If you punch it into your calculator, you'll find that it evaluates to 0.809016994, which is half of the golden ratio. However, it would be nice to have an algebraic proof, right?

I worked through the algebra, but typing it all out on the blog would be UGLY, so I'm just going to post an image of the work I did on paper.

To view a larger version of this image, just click on it.

When I got to the end of the algebra, I had a radical within a radical, which is an ugly looking beast, but I happened to remember that (3 + SQR(5))/2 is the square of the golden ratio, which made the whole thing simplify quickly.

Is there an easier way to arrive at the cos(36º)? I'm sure there is. This was just the first one that came to mind. There might be other ways to do this using the law of cosines, or the law of sines, and I know you can do it with an entirely non-geometric proof (using various trig identities) but this one does the job. If you find a simpler proof, let me know!

Fourth grader Alice asks, "How many diagonals are in decagon?"

Great question, Alice. But instead of giving you an answer to that question, I'm going to show you how you can figure it out for yourself. And not only that, I'll show you how you can figure out the answer for any polygon, even if it has 20, or 50, or 2000 sides!

Ready? Let's start with a simple example. We'll go with a polygon that has 8 sides (which is called an octagon), like this:

Now, this polygon, because it has eight sides, also has eight vertices. It seems a bit overwhelming to try to figure out all the diagonals, so let's just focus on one vertex. How many diagonals can you draw in an octagon, that all begin at one vertex?

The answer to that question is five. Take a look at the diagram below:

In this diagram I've chosen the diagonal to the left just below the top vertex, and I've drawn diagonals to every vertex that I can draw a diagonal to. Which diagonals can't I draw diagonals to? Well, I can't draw a diagonal from a vertex back to itself, and I can't draw diagonals to the two vertices next to that one (because those wouldn't be diagonals; they'd be sides!).

So there are three vertices I can't draw diagonals to from that vertex. Eight vertices total, minus the three I can't draw to, leaves five. That's important to remember: subtract 3 from the number of vertices, and you have the number of diagonals you can draw from any vertex.

But that's just one vertex! You could draw diagonals from any vertex, right? Sure! And there are eight vertices in our octagon, so we take the number of diagonals per vertex, and multiply it by the number of vertices: 5 x 8 = 40.

You might be tempted to think that that's our answer, but it's not. Why not? Because we've counted every diagonal twice! Every diagonal has two vertices, so we've counted it from one end, and we've also counted it from the other end. So to get the actual number of diagonals, we have to divide our answer by 2. 40 / 2 = 20. There are twenty diagonals in an octagon.

Let's try that reasoning on a polygon that has 2000 sides. Now, I'm not going to draw a 2000-gon for you; we'll just have to work out the reasoning without a picture.

1. Pick a vertex. How many diagonals can you draw from that vertex? Answer: 2000 - 3 = 1997.
2. How many vertices total? Answer: 2000
3. How many diagonals counted from all the vertices? Answer: 1997 x 2000 = 3,994,000
4. Oops! We've counted each diagonal twice! How do we get rid of the duplicates? Answer: 3994000 / 2 = 1,997,000

So a 2000-gon has 1,997,000 diagonals!

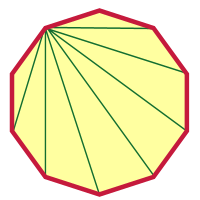
After doing something as crazy as a 2000-gon, a decagon shouldn't seem so difficult, right? I'll get you started, and you can finish it from here. I picked a vertex and drew diagonals from that vertex.

How many are there? Were you able to figure out how many there were without looking at the picture?

Can you figure it out from here? I hope so! Good luck, Alice. 

By the way, there is a formula you can use; it looks like this: D = n(n - 3)/2. But honestly, I don't expect my students to memorize it. I expect them to remember how we reason it out here. If you understand the logic, it's even better than having a formula!

Every year that I teach Physics I run into a small problem with the labs my students do. Here's the problem. My students will collect data (and the issue happens most often when they're timing something) and then they'll look at their data and say, "Wow! One of those points is way off from the others!"

For example, their data points might be the following times in seconds: 4.2, 4.6, 4.3, 4.8, 7.2, 3.9

As they look at those data points, they'll recognize that most of them are in the vicinity of 3.9 to 4.8, but there's one value (7.2) that is way off from the others. Obviously something went drastically wrong with that trial!

So what do I tell them? I'd like to tell them, "Use your statistics knowledge to determine the outliers." Outliers are points like 7.2, which are clearly outside the reasonable range. That's what I'd like to tell them, but I don't, because I know perfectly well that many high school science students have not yet learned enough statistics to calculate outliers.

And I have no intention of spending my Physics class time teaching statistics!

So what do I do? I say to them, "If it looks ridiculous, dump it."

Now, that's a quick approach, and it saves a lot of time, but it's not really a "good" approach (although I'm not the only science teacher that does it!). Why is not a good approach? Because good scientists try to avoid using intuition and guesswork when selecting their data. That kind of fuzzy thinking can result in people massaging their data to make it say exactly what they want it to say.

So this year, I decided it was time to resolve that problem. Not by teaching my students how to find quartiles, interquartile ranges, and outliers. No...I decided to create a calculator that they could enter their data in, and have the calculator list their outliers.

And, while I was at it, since I realize these kinds of tools can be very helpful for both teachers and students, a whole section of statistics calculators was added to the site. These include calculators for various means (arithmetic, geometric, and harmonic), as well, as standard deviation, variance, and other useful statistical quantities.

You can find the calculators here: Professor Puzzler's Statistics Calculators.

Twelfth grader Abbey wants some help with the following: "Factor x⁶ +2x⁵ - 4x⁴ - 8x³ + x² - 4."

Well, Abbey, if you've read our unit on factoring higher degree polynomials, and especially our sections on grouping terms and aggressive grouping, you probably realize that a good way to attack this problem is to try grouping the terms. Hopefully, you tried something along those lines. Here's one method (I'll get you started on another method at the end of this post):

(x⁶ + 2x⁵) - (4x⁴ + 8x³) + (x² - 4).

That looks promising, since every group can be factored:

x⁵(x + 2) - 4x³(x + 2) + (x - 2)(x + 2).

Great! every group has an (x + 2) term in it, so we can factor that out:

(x + 2)(x⁵ - 4x³ + x - 2)

I'm going to attempt grouping on that second polynomial:

(x + 2)[(x⁵ - 4x³) + (x - 2)]

(x + 2)[x³(x² - 4) + (x - 2)]

(x + 2)[x³(x - 2)(x + 2) + (x - 2)]

And once again we have a common factor in our groups - this time it's (x - 2).

(x + 2)(x - 2)[x³(x + 2) + 1]

(x + 2)(x - 2)(x⁴ + 2x³ + 1)

Now we have something that can't easily be grouped, because it has 3 terms. So I decided to try something crazy: I added in x² and subtracted it back out again. Why? Take a look:

(x + 2)(x - 2)(x⁴ + 2x³ + x² + 1 - x²)

(x + 2)(x - 2)[(x⁴ + 2x³ + x²) - (x²- 1)]

(x + 2)(x - 2)[x²(x² +2x + 1) - (x + 1)(x - 1)]

(x + 2)(x - 2)[x²(x + 1)² - (x + 1)(x - 1)]

My groups each contain an (x + 1), so I can factor that out:

(x + 2)(x - 2)(x + 1)[x²(x + 1) - (x - 1)]

(x + 2)(x - 2)(x + 1)(x³ +x² - x + 1)

At this point, I tried a couple different groupings, and nothing seemed to work to factor (x³ +x² - x + 1). That doesn't mean it's not factorable, but I got a little suspicious, so I pulled out the Rational Root Theorem, which tells me that if that thing has any rational zeroes, they have to be either 1 or -1. Since neither of those are zeroes of the polynomial, that means it's unfactorable over the rationals. Therefore, the final answer is:

(x + 2)(x - 2)(x + 1)(x³ +x² - x + 1)

Just a couple notes on this, before I'm done:

1. I enjoy the process of trying to do grouping (and what I call "aggressive grouping") on polynomials in order to factor them. I think it's a good mental exercise. Nevertheless, I should point out that according to the Rational Root Theorem, if this polynomial has any rational zeroes, they are any of the following: -1, 1, -2, 2, -4, 4. Trying out those to see which work, and then using Synthetic Division to divide out the factors will guarantee you a solution, even if you can't figure out groupings to do.
2. There's another way to start off the problem (which is actually what I did the first time I solved the problem), which involves rearranging the terms before grouping: (x⁶  - 4x⁴) + (2x⁵- 8x³) + (x² - 4). Grouping this way has the advantage of pulling out (x + 2)(x - 2) all in one step, and going straight to a 4th degree polynomial. It's nice to see that the problem can be done in multiple ways, don't you think?

"Hi Professor Puzzler, in last week's post you said that if a number is irrational, it doesn't terminate or repeat. I wonder how you know that? Of all the irrational numbers, how do you know there isn't one that terminates or repeats?"

This question comes from Trevor in Georgia.

Hi Trevor, in answer to your question, I'll give you a short proof (with a bit of hand-waving over some details, just to keep the write-up from being too long!). What we'll do is, we'll start with numbers written in decimal notation, which we'll assume are irrational (which means, as you remember from the post about the square root of two, that it can't be written as a ratio of integers) and then we'll arrive at a contradiction, which will prove that they aren't irrational. So let's get started!

Terminating Decimal

Let n be an irrational number with a terminating decimal. This means that after a certain number of decimal places (let's call that k), the decimal ends.

Since the decimal terminates after k decimal places, the number 10^kn is an integer (every time you multiply by 10, you shift the decimal one place to the right, so multiplying n by 10^k results in all the digits being to the left of the decimal).

Now we can write n = (10^kn)/(10^k), which is ratio of two integers, and that contradicts our original assumption that n was irrational. Thus, if a number in decimal form terminates, it is not irrational.

Repeating Decimal

Let n be an irrational number with a repeating decimal. This means that after a certain number of decimal places (let's call that k), the decimal begins repeating every h digits, where h is some integer.

For example, if the number is 3.125727272..., k = 3, h = 2.

To simplify our math, let's multiply our number by 10^k, which allows us to get the non-repeating part of the decimal over to the left of the decimal. We understand that when we're done with our manipulations, we have to divide by 10^k to get our number back, but if we've proven that our result is rational, then dividing by 10^k still gives us a rational number.

Similarly, everything to the left of the decimal can then be subtracted, with the understanding that when we're done we must add it back in. But the same argument holds; if we've proved the result is rational, adding an integer to that rational number will result in another rational number.

In other words, we can, without loss of generality, simplify our starting point to a decimal which looks like this:

n = 0.a₀a_1...a_ha₀a_1...a_ha₀a_1...a_h...

Let m be the integer formed by the following digits: a₀a_1...a_h

Then n = m/(10^h) + m/(10^2h) + m/(10^3h) + ...

This is an infinite series with common ratio 1/(10^h), and its sum is:

S = [m/(10^h)]/[1 - 1/(10^h)]

S = m/(10^h - 1)

Since m is an integer, and 10^h - 1 is an integer, we've shown that our number can be expressed as a ratio of integers, which contradicts our assumption that it is irrational. From this we've shown that if a decimal repeats or terminates, it is not irrational.

Thanks for asking, Trevor!