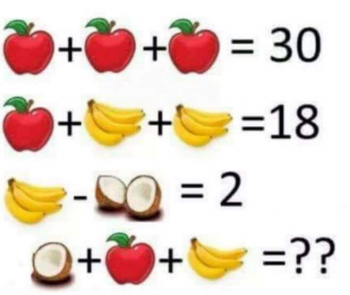Vusi from South Africa wants to know - if you roll a blue die and a yellow die, why are these considered to be independent events?

Well, Vusi, let's start off by making sure we understand the terms "dependent events" and "independent events."

Dependent Events
Two or more events are dependent if the outcome of one of the events will affect the outcome of the other.

For example, if you have a jar that contains 100 blue jelly beans and 100 yellow jelly beans, and you draw one jelly bean and eat it. The probability that the jelly bean will be blue is 0.5 (100/200, because there are 100 blue jelly beans and a total of 200 jelly beans all together). However, if you then draw a second jelly bean from the jar, the probability of it being blue is not 0.5. In fact, we really don't know what the probability is. Why? Because if the first draw was a blue, the probability will be 99/199 (because we have one less blue, and one less total), but if the first draw was yellow, the probability of a blue on the second draw will be 100/199 (because we still have 100 blues, but one fewer yellow). Thus, the probability of the second event can't be calculated without knowing the result of the first event. The first event affects the outcome of the second event. These are therefore dependent events.

Independent Events
Two or more events are independent if the outcome of one event has no effect on the outcome of another.

To keep this simple, let's talk about the same jar. Only this time, instead of eating the jelly bean, you put it back in the jar after drawing it out. The probability that the first jelly bean drawn is blue is 0.5. But what about the second drawing? In the second drawing, you still have 100 blue jelly beans and a total of 200, because the first jelly bean drawn was put back in. Thus, it makes no difference what you draw the first time; the probability for the second draw being blue is still 0.5. The first draw does not affect the second draw, so these are independent events. 

Hopefully, with this in mind, you can answer your own question. Are the rolls of a blue die and a yellow die independent? Yes they are! Because the roll of the blue die is not going to affect the roll of the yellow die. The yellow die isn't going to think, "Oh, the blue die is showing a 3, so I better not land on 3," or "The blue die is showing an even number, so I should show an odd," or "Hey, the blue die is showing a 6, so if I land on 6 we'll have doubles!" Whatever happened with the blue die has absolutely no bearing on what happens with the yellow die. Therefore, these are independent events.

By the way, we have a reference unit on probability on this site, which you can find here: Probability concepts and problems. This unit contains a section on independent events and dependent events, so you can read more on that here: Independent Events, Dependent Events.

Thanks for asking!

S. from Utah asks, "Why do math teachers make us simplify radical expressions?"

Great question, S! The good news is, we have a unit on "Simplifying Radical Expressions" in our reference section, and the unit has a page that answers your question! If you visit this page right here: Why We Simplify Radicals, you'll get an explanation for some of the reasons.

The short answer is: There are multiple ways of writing the same number, but if we all follow the simplification rules, we'll all write our answers the same way, which makes it easier for people to work together, if they're all expressing their work in the same way.

Here's another way of looking at it: suppose you lived at 12 Main Street. Which of the following pieces of mail are addressed to you?

• 12 Main St
• SQR(144) Main St
• 2SQR(36) Main St
• 4SQR(9) Main St
• 3SQR(16) Main St
• SQR(9)SQR(16) Main St

Which of these pieces of mail are addressed to you? Well, obviously the first one is, but even though the others might not look like it, they all actually evaluate to 12 Main St. But the big question is: how many of them will actually get delivered to you? The answer is probably, "It depends on how much of a sense of humor the postal workers have!"

The reality is, if we don't simplify our answers so they all look the same, we make a lot of extra work for someone. Right now, that someone is your teacher (who has to grade your tests and homework), but if you pursue a career in a STEM field, the someone will be you, and the people on your team.

So practice simplifying those radicals until it becomes second nature. Your teacher will thank you now, and someday future-you may thank you as well!

Judah asks: "A Highly Composite number is a number that has more factors than any other less than it (positive, whole numbers). Like 12 has 6 factors, which is more than any other below it (whereas 1 has 1 , 2 has 2, and so on). Is there an equation to tell if a number is highly composite? If no, than I might find one. :P But is there?"

Hi Judah,

I'm not familiar with an actual formula that you could use (something along the lines of a function that you plug n into it and you get the n^th highly composite number out). However, there are some tips I can give you for finding highly composite numbers (short of looking up a list on a website somewhere).

First, it's important to note that what really matters in highly composite numbers is the exponents in their prime factorization. Why? Because the number of factors a number has can be directly calculated from those exponents. Let me show you how.

Take the number 72. How many factors does this number have? We can find out by simply testing numbers to find out if they're factors:

1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72

72 has twelve factors.

But there's another way to find out how many factors 72 has. Write the prime factorization of 72:

72 = 2³3²

Now consider the fact that every factor of 72 contains both powers of 2 and powers of 3. For example, 12 = 2²3¹, 18 = 2·3². This is also true of 1, though you might not think so at first: 1 = 2⁰3⁰. Similiarly, 8 = 2³3⁰.

But, of course, if a number has 2⁴ or 3³ as part of its prime factoriztion, the number can't be a factor of 72, because it has too many twos, or too many threes.

We can look at it this way: if a number is a factor of 72, it contains in its prime factorization either 2⁰, 2¹, 2², or 2³. Similarly, the prime factorization contains 3⁰, 3¹, or 3².

There are 4 ways to choose how many twos to include, and 3 ways to choose how many threes to include to build a factor of 72. If you've studied counting principles at all, you know that the total number of ways to create a factor is then 4 x 3 = 12, which matches the number we obtained by listing factors.

Let's try another example: How many factors does 6,615 have? I'm sure you don't want to try to list them all by hand, right? So let's try our other method. Prime factorization of 6615 = 3³5¹7².

Thus, there are 4 ways to choose how many threes, 2 ways to choose how many fives, and 3 ways to choose how many sevens to include in a factor. Therefore, there are 4 x 2 x 3 = 24 factors.

So how do we use this to help us find highly composite numbers? Well, we can use it indirectly, because we can use this to help find the smallest number that has n factors.

Let's say we want to find the smallest number with 15 factors. Well, 15 can be factored in two ways:

15 = 15 x 1
15 = 3 x 5

Using the first factorization is going to result in a ridiculously large number (2¹⁴3⁰), so should use the other way of factoring. We need to have a prime factorization that includes an exponent of 2 and an exponent of 4 (2 is one less than 3, and 4 is one less than 5). We'll get our smallest number by assigning the largest exponent to the smallest prime factor, which gives us 2⁴3² =  144. 144 is the smallest number with 15 factors.

What if we wanted to find the smallest number with 16 factors? There are many more possibilities here, because 16 can be factored in several different ways:

16 = 16 x 1
16 = 8 x 2
16 = 4 x 4
16 = 4 x 2 x 2
16 = 2 x 2 x 2 x 2

Each of these gives rise to a different number:

16 = 16 x 1            21530 = 32768
16 = 8 x 2             2731 = 384
16 = 4 x 4             2333 = 216
16 = 4 x 2 x 2         233151 = 120
16 = 2 x 2 x 2 x 2     21315171 = 210

Of these 120 is the smallest, so 120 is the smallest number with 16 factors.

Notice that the smallest number with 16 factors is actually smaller than the smallest number with 15 factors, which means there is no highly composite number with 15 factors. You can't assume that 120 is a highly composite number, either, until you've done some more testing, but if I had to make a guess, I'd say it probably is. Okay, I just checked a list on Wikipedia, and 120 is a highly composite number.

Hopefully this will inspire you to more exploration, and maybe you'll find that formula you were looking for. Thanks for asking!

Esther from Georgia wants to know "Why do extraneous solutions happen in math problems?"

Extraneous solutions are solutions which are obtained algebraically, but even though they are found algebraically, they don't work in the context of the problem. Here are some of the reasons a problem might have extraneous solutions. For each reason, I'll give an example.

Real World Restrictions

Sometimes a solution that we find algebraically is extraneous because it doesn't fit real world restrictions on the solution. For example, consider the following problem:

A rectangle's length is 2 more than its width. Its area is 48 square feet. What is the rectangle's width?

To solve this, we say, let w equal the width. Then we have: w(w + 2) = 48

This is a quadratic equation: w² + 2w - 48 = 0, which leads to w = 6 or w = -8. However, the real world restriction on the solution is that w is the width of a rectangle, and rectangles can't have negative side lengths. Therefore, -8 is an extraneous solution.

Problem Restrictions

In other cases, the problem itself might set restrictions on the solution.

Find all two digit numbers such that when the number is squared, and ten times the number is subtracted, the result is 11.

This problem leads to the quadratic: x² - 10x - 11 = 0

(x - 11)(x + 1) = 0

x = 11 or x = -1.

But the problem itself sets the restriction that x must be a two digit number, so x = -1 is extraneous.

Division By Zero

Sometimes a problem has fractions, and a number that works out algebraically actually causes a division by zero, which is illegal, immoral, and socially unacceptable. As a problem writer for math competitions, I like to deliberately create problems in which this happens, because the very best students check their solutions and realize they've got an extraneous solution. Here's a very simple example:

(x + 1)/(x - 1) = 2/(x - 1)

An easy way to solve this is to multiply both sides by (x - 1), which gives x + 1 = 2, or x = 1. But the process of multiplying by (x - 1) has made a fundamental change to the problem; we no longer have a denominator. If we go back to the original problem and try to plug x = 1 into it, we find that we have a division by zero, and therefore x = 1 doesn't actually work; it's extraneous.

Principle Roots

Each positive number has two real square roots. For example, the square roots of 4 are 2 and -2. However, when we write radical notation, we are, be definition, referring to the principle square root, which is the positive value. Thus, a solution may be extraneous because it results from using a negative square root instead of the principle square root. Here's an example:

√(x)  = x - 6

To solve this, we square both sides:

x = x² - 12x + 36

Rearrange, simplify, factor, solve:

x² - 13x + 36 = 0

(x - 9)(x - 4) = 0

x = 9 or x = 4

Now, plug 9 into the original equation, and you'll see that it does work. But what happens when you plug in 4? You get a false equation! But why does that happen? Because on the left-hand side, 4 has two square roots, and one of them (-2) does work. So it's our own choice to define √(x) as the positive square root of x that results in the extraneous solution.

Are there other causes for extraneous solutions? Probably, but that should serve as a simple crash course on the common ones you'll see in an algebra class.

I'm Glad I've Got a Proofreader

In addition to occasionally writing math problems for this website, I've also written math problems for several states' math competitions. When I sit down to write problems, it's usually because I have to crank out a set of 100 math problems for a competition somewhere. When I'm finished writing them, I send them off to my proofreader. When he's proofreading, what do you suppose he's most likely to find?

1. spelling mistakes
2. grammar mistakes
3. arithmetic errors
4. algebraic errors
5. ambiguity errors

He does occasionally find spelling/grammar mistakes, but those are fairly infrequent. And yes, I do occasionally have arithmetic/algebraic errors! (When I'm writing a problem, sometimes I have to try two of three different things to make the problem work out correctly, and then I forget which things I've changed, and use numbers from the first version of the problem, and then my proofreader says, "Where in the world does this number come from?")

But the most common issue he finds is an ambiguity issue. Ambiguity simply means that students could reasonably interpret the problem in more than one way. If the student could interpret the problem in multiple ways, then it's a bad problem!

Here's a simple example:

In a right triangle, the sides are 5, x, and x + 1. Find the length of the hypotenuse.

Why is this ambiguous? Because I've implied that there's one answer ("find the length" instead of "find all possible lengths") but there are two possible answers, because the hypotenuse could be 5 (if x and x + 1 are less than 5) or it could be x + 1 (if x + 1 is greater than 5).

Here's another example:

Find the next term in this sequence: 5, 10, 15, ...

The obvious answer is 20, but that's not the only possibility; someone who is familiar with Fibonacci sequences could argue that this is the beginning of a Fib, and therefore the next term is 10 + 15 = 25.

These are just simple examples. The more complicated a problem is, the more likely it is to introduce something ambiguous without meaning to. So I'm glad I've got a problem proofreader.

The Internet Has No Proofreader

Now I put on my other hat - the "Professor Puzzler" hat. On any given day, this blog is a pretty quiet corner of the internet. This blog usually gets just a few hundred visitors per day. (Except on days we publish a new post, then the visitor rate climbs a bit).

But every once in awhile, something goes crazy. Back in February, for instance, there was one day where the traffic to the Professor Puzzler blog was 100 times it's normal rate. We had over 25 thousand page views on just one page of the blog.

Whenever this happens, it's invariably because someone posted an ambiguous (bad) math problem on the internet, and someone linked to our explanation of why it can't be solved.

And I realized something, after the most recent one: the majority of math problems posted on social media are ambiguous. The internet has no proofreader.

If you're interested to see some of the ambiguous/bad problems we've talked about in this blog, here are links to some of them. Just click on the image to jump to the corresponding blog post.

The most recent one was "The Flower Problem" or (as one site called it) "Pollen Pandemonium." This problem is straight-up ambiguous (and no, it was not part of a kindergarten exam in China; give the Chinese some credit, will you?). The most appropriate interpretation is to say that each distinct flower image represents a different variable. If that's the case, you have a system of three equations in four unknowns, which is unsolvable. If you operate from the assumption that the problem must have a solution, you reject the most appropriate interpretation, and then there is no way to solve it without making an assumption about what the writer intended. Each assumption will lead you to an answer, but depending on the assumption you make, you'll get a different answer. So the internet is full of people arguing for their interpretation, when the reality is, every solution is based on an unwarranted assumption.

The square problem is also ambiguous in the same way that my sequence problem above is ambiguous; there are multiple ways of interpreting the intent of the problem writer, and there isn't one right answer; there are many possible answers. But the problem is great for click-bait sites, because people will spend all day arguing their answer in the comments.

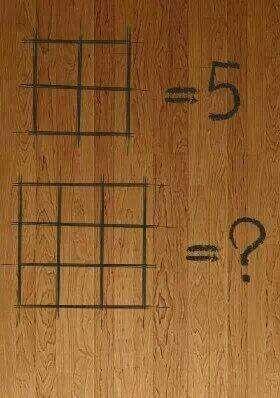
And there you have it: a history of bad math problems on the Ask Professor Puzzler blog. Click-bait sites love problems like this, because they generate arguments, and arguments turn into page views, comments, likes, and notoriety.

Math teachers, on the other hand, hate them...except as teaching tools about ambiguity!

Update June 20, 2016: One wise commenter responded to this blog post by saying "So people would rather argue, pretending unsolvable problems are solvable, than accept the simple fact that the problem was badly phrased to begin with. Seems this could have applications to Internet interactions far beyond the math realm!"

Can't argue with that!