Before getting to the question for this morning, I'd like to direct your attention to our simulation of a game show with three doors. It's called the "Monty Hall Game." Understanding this game will be important to thinking about Tracie's question below.

The short summary of the game: There are three doors, and only one of them has a prize behind it. You pick a door. Then Monty opens another door to show you that it's empty, and asks you if you want to switch your guess. What do you do?

Tracie from South Dakota asks, "So if the game show host opened 2 doors for me, would I still have 1/3 probability of winning?"

Hi Tracie, your question highlights a couple of the things about the Monty Hall game that often causes confusion. 

1. Monty Hall knows in advance where the pot of gold (or new car, or whatever) is. The rules of the game are that he opens an empty door. But if he always opens an empty door, that means he knows where the empty doors are. That's an important concept to understand. He's not being entirely random in his choice of doors to open. There are two empty doors, so if you pick one of them, he picks the other. The only time he's being random is when you pick correctly; in that circumstance he randomly picks one of the empty doors to open.
2. This is not a static problem - the circumstances change, and because the circumstances change, the probabilities could change as well. Let me give you an example. Suppose that during Christmas vacation, we decide we want to take our kids sledding. Since I'm not teaching that week, I can pick any day of the week to go. So we would say that my probability of picking Tuesday is 1/7 (there are seven days in a week, and Tuesday is one of them). Now suppose that my wife looks at a weather forecast, and says, "Oh! Thursday, Friday and Saturday are supposed to be cold, with a wind chill of -20 F!" If I use that information in making my choice, what is my probability of picking Tuesday now? It's 1/4, because we've eliminated 3 of the 7 days. That doesn't mean the original 1/7 is wrong - it means that the conditions of the problem have been changed, and so we have to calculate a new probability. This is not, by the way, a perfect analogy to the Monty Hall problem, so please don't try to make it match. The differences are:
   1. We're talking about the probability that I'll pick a certain day, not the probability that the day I pick is a good one.
   2. We don't know that there's only one good sledding day.
   3. My wife is not deviously hiding known information from me.
   4. Weather forecasts are not 100% accurate anyway.
   5. There is no #5, but at the end of this post, I'll - just for fun - turn this example into a better analogy for the Monty Hall Game.

Okay, so how does this relate to your question?  Number two should be fairly obvious; we have a change in conditions, so there's no reason to assume that the probability will stay the same. The probability of you winning WAS 1/3, but the changing conditions mean we have to recalculate the probability.

But here's the more important issue. Monty Hall can't play the game the way you suggest. Why not? Because if the rules of the game are "Monty will open two empty doors," Monty is going to run into trouble every time you don't pick the right door. Because if you pick the wrong door, how many empty doors are there left for Monty to open? Only one! If you pick one of the empty doors, then there's only one other empty door for him to open.

If he opens two doors, that means you've picked the correct door.  So even though your original choice was 1/3 probability of winning, under the new circumstances, you have a probability of 1 (100% chance) of winning.

If you're wondering how that number 1/3 fits into the solution it fits like this: The probability that Monty can open two doors is 1/3 (the same as the probability that you selected correctly). So the number 1/3 is still in there - just in a different place!

If you're wondering why the probability changes in this case, but doesn't when he opens one door, the answer is this: When he opens just one door, he has not given you any information about the door you opened. When he opens two doors, he has (indirectly) given you information about your door.

To add to this, the only way Monty could do the two-door rule would be to have to have a pair of rules:

1. If you pick the right door, he will open two doors. (this happens 1/3 of the time)
2. If you pick the wrong door, he will open one door. (this happens 2/3 of the time)

The problem with this is: if you know the rules, you can do an always-winning strategy. If he opens two doors, you've automatically won, and if he only opens one door, that means you picked the wrong door, so you must swap.  Monty would DEFINITELY not want to play by those rules!

Addendum: If you would like to look at a couple different ways of understanding the Monty Hall problem, you can find more write-up here: The Murky Swamp of Probability.

Sledding in December. Let's say my wife looked at the weather forecast and told me, "Every day but one this week is going to have a wind chill of -20 F, and there will be one day that's going to be sunny and warm. So, randomly pick a day for sledding." (My wife hates the cold, so she would definitely not do something as ridiculous as that!) We'll make the wild assumption for this example that the National Weather Service has 100% predictive accuracy.

So I pick Tuesday. I have a one-in-seven chance of "winning," based on the information I have. Of course, my wife has a different perspective, because she has more information than I do. She knows with 100% certainty whether I've picked correctly or not!

Now my wife says, "Okay, I'll tell you that the following days are going to be -20 F: Sunday, Monday, Thursday, Friday, Saturday."

She's narrowed my choices down to two possibilities. But it's important to remember that this was not a completely random choice. She didn't pick 5 out of 7 days to eliminate; she picked 5 out of 6! She couldn't eliminate Tuesday, because that was the day I had picked, and if she eliminated it, I would be forced to change.

My reasoning now goes as follows: Based on my original information I was given, Tuesday had a 1/7 probability of being the best day for sledding.  That means there was a 6/7 probability that one of the other days was the good sledding day. So there's a 6/7 probability that the good sledding day is: Sunday, Monday, Wednesday, Thursday, Friday or Saturday. As a probability equation, I could write:

P_su + P_m + P_w + P_th + P_f + P_sa = 6/7

But now my wife has changed the problem. She's changed it by giving me more information: She's told me the values of all but one of those probabilities is zero!

That means: 0 + 0 + P_w + 0 + 0 + 0 = 6/7, which means that P_w = 6/7!

So do I switch my decision to Wednesday? You bet I do! The key to understanding this is that my wife's choice of information to give me is not random, and it therefore significantly alters the shape of the problem.

I hope that this is a helpful answer. The Monty Hall problem is one that repeatedly trips people up. I wonder if my blog post will increase the probability of people not getting tripped up by it!

PS - if you go to the Monty Hall game and change the game settings to 7 doors, 5 hints, that will be the same as my sledding example. Turn on the automation, and watch the percent. If you let it run long enough, you'll see that it eventually settles down to about 85.7%, which is the 6/7 probability we calculated.

Fourth grader Zaq asks the question, "If 6 times 6 equal 36 why doesn't 7 times 5 do the same?"

That's a great question Zaq. One of the easiest ways to understand multiplication is to think of it with pictures. Below, I show a picture of a 36 boxes in a great big square. The square has six rows and six columns.

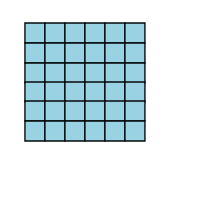
We say that 6 x 6 = 36 because if you have six rows, and each row has six objects in it, that's a total of 36 objects.

You can check it for yourself, by counting up all of those individual boxes in the picture. You'll find that there really are thirty-six of them.

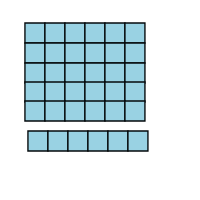
But what about 7 x 5? If you had five rows, and there were seven objects in each row, would there be 36 objects? Well, let's find out. First, I'm going to take the row off the bottom, which will give us five rows instead of six.

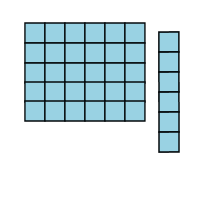
Now I'm going to take that row and rotate it around so it'll fit on the side of the picture.

Uh oh...you see what's going to happen, right? We're going to have an extra block! There are two many rows in that group of boxes, so there'll be one poor little box, all stuck by himself, that doesn't fit into the picture.

And that one block shouldn't come as a surprise to you, because you know what 7 x 5 is - it's 35, which is one less than 6 x 6! And sure enough, that "one less" is the reason why we have a leftover box at the end.

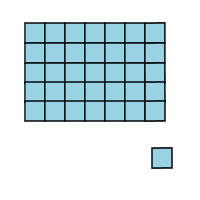
You might also be interested to know that that "one less" idea also works whenever you multiply a number by itself: 7 x 7 is 49, but 6 x 8 is one less than that. 10 x 10 is 100, but 9 x 11 is one less than that. 12 x 12 is 144, but 11 x 13 = 143. It's easy to see why that is; whenever you try to take a perfect square and turn a row into a column like we did above, you'll end up with one extra block!

And someday, you'll take an alegbra class, and you'll learn a different way of explaining why that works, but for now, hopefully you'll find the picture a good way of understanding it. Thanks for asking!

9th grader Akhil from Kerala asks the following: "The sides of a quadrilateral are extended to form exterior angles. Find the sum of these exterior angles."

Hi Akhil, instead of just answering the question you asked, I'd like to explore the question in a little more depth, and explain why the answer is what it is. After all, if I just told you the answer, that would make for a pretty boring blog post!

So let's start off with a quadrilateral. I'm going to show you a picture of one below, and ask a question about it. How many degrees are there in the measures of all the interior angles of the quadrilateral?

Now, you might already know the answer to that question; the sum of all the interior angles is 360 degrees. But can you prove that to be true? It's actually not hard to understand why that quadrilateral (and all quadrilaterals, for that matter) have an interior angle sum of 360 degrees. To see why, just look at this picture, in which I've divided the quadrilateral into triangles:

How many triangles did it take to divide up that quadrilateral? It took two, right? And how many degrees does each of those triangles have? 180 degrees. And so altogether, how many degrees do they have in total? 180 x 2 = 360 degrees.

Understanding that the total of the interior angles is 360 degrees is important to finding the number of degrees in the exterior angles. Here's a picture that shows what you described - the sides being extended to form exterior angles:

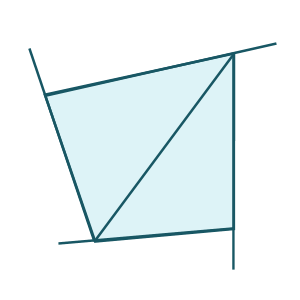
By extending these sides, we've created linear pairs - pairs of angles that form a straight line. Each linear pair includes an interior angle and an exterior angle. Each linear pair adds to 180 degrees (a straight line), and there are four linear pairs (because there are four sides).

So if there are 4 linear pairs, and each linear pair is 180 degrees, that's a total of 720 degrees. But 360 degrees of that is interior angles, so the exterior angles have to add up to 720 - 360 = 360 degrees! And that's your answer.

Now, it might be tempting to think that the interior angles of a polygon and the exterior angles of a polygon will always match, since they do in the case of a quadrilateral, but that is not the case. Let's take a look at a pentagon to see why. Here I'll give you a pentagon divided into triangles, and with sides extended:

In the case of a pentagon, we can divide the polygon into 3 triangles, which means the interior angles add to 3 x 180 = 540 degrees.

We've created 5 linear pairs, which total 5 x 180 = 900 degrees.

Since there are 900 degrees total, and the interior angles add to 540 degrees, the sum of the exterior angles is 900 - 540 = 360 degrees!

It turns out that the sum of the exterior angles is 360 degrees regardless of whether it's a quadrilateral or a pentagon.

What do you think...can you generalize it even further? How many degrees are there in the interior of an n-gon? And how many degrees in the exterior angles of an n-gon? I'll leave it to you to figure that out. Thanks for asking, Akhil!

Emmanuel from Papua New Guinea asks, "How do find the common ratio of a geometric sequence if the ratio of the fourth and second term are given?"

Well, Emmanue, the short answer is: you can't!

Let's suppose the second term of geometric is 4, and the fourth term is 16. You might think, "Oh, that's easy - the ratio must be 2, because 4 x 2 is 8, and 8 x 2 = 16!" But that's not necessarily true - maybe the ratio is -2! 4 x -2 = -8, and -8 x -2 = 16. 

The problem is, in a geometric sequence, all the even-numbered terms will have the same sign, but that won't tell us anything about the sign of the odd-numbered terms, and that information is needed to find the ratio. But we can set up an equation that'll give us the possible values.

Let's say the second term is 2, and the fourth term is 18. Then 

ar = 2, and ar³ = 18

If we rewrite the second equation as ar(r²) = 18 we can subsitute the first equation in place of ar, giving:

2r² = 18, or 

r² = 9.

Now, it's tempting at this point to say, if r squared is 9, then r must be 3, but you're missing a possibility if you do that, because 9 has two square roots: 3 and -3. These are your two possible ratios. We don't know what the ratio is, but at least we've narrowed it down to two possibilities!

By the way, as a side note, in order to get my students to avoid missing a solution in an equation like r² = 9, I tell them they have to solve the equation like this:

r² = 9
r² - 9 = 0
(r - 3)(r + 3) = 0

Therefore r - 3 = 0 or r + 3 = 0, which leads to r =3 or r = -3.

It's more work, but it keeps them (most of the time) from forgetting a root!

Question: an arithmetic mean of two numbers is always between the two numbers being averaged. Is this also true of harmonic means and geometric means?

Yes, it is. Let's take a look at both types of means, and see if we can figure out why. In each case we'll make the assumption that we're taking the mean of two positive, distinct numbers. Positive, because goeometric means and harmonic means are generally defined to be over the set of positive reals, and distinct, because having non-distinct numbers makes the mean equal to the original number, which isn't terribly interesting.

Geometric Mean

The geometric mean is the square root of the product of the two numbers. So if the numbers are a and b, then the geometric mean is SQR{ab}.

We will say, without loss of generality, that the two numbers are a and b, with a < b.

Multiply both sides of the equation by b:

ab < b²

Taking the square root of both sides gives SQR{ab} < b

Similarly, if we multiply the first equation by a, we get:

a² < ab, or a < SQR{ab}

Therefore, a < geometric mean < b.

Harmonic Mean

The harmonic mean is the reciprocal of the average of the reciprocals, or 2ab/(a + b). Again, we'll assume, without loss of generality that a < b.

Multiply both sides of this equation by a, and then add ab:

a² + ab < 2ab

Now factor the left side:

a(a + b) < 2ab.

Finally, divide both sides by (a + b):

a < 2ab/(a + b).

We can repeat the process on the other side:

a < b
ab < b²
ab + ab < b² + ab
2ab < b(a + b)
2ab/(a + b) < b

Therefore, a < harmonic mean < b