Horizontal Stacker

Instructions

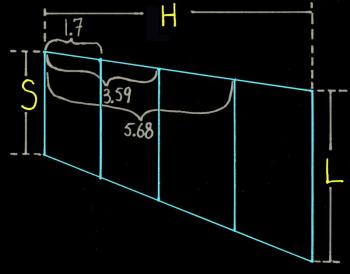
Refer to the diagram below to understand the information needed by the calculator. The diagram is a sample that uses the default values which appear in the calculator.

• H: The length of your horizontal line segment (of course, this segment is actually diagonal, unless it happens to be on your horizon line).
• S: The length of your shorter segment representing a vertical side. This is the side closer to the vanishing point.
• L: The length of your longer segment representing a vertical side. This is the side further away from the vanishing point.
• N: The number of horizontal divisions (in the sample image, N = 4, because it's split into four pieces).
• The only time your surface will have congruent horizontal segments is when the surface is centered on the horizon line. Therefore, it's important to remember that whichever side you measured, that's the one you mark on. From there, simply draw vertical segments to the opposite side.
• Although this calculator was designed for perspective drawing with 2 vanishing points, it should also work for 3 vanishing points. In 3-point perspective, however, you will not have a trapezoidal surface, but a quadrilateral. In this case, since none of the division marks will be parallel to the vertical sides, it will be necessary to provide one horizontal length, and then the other, and measure distances at both top and bottom of the surface.

What's the Point?

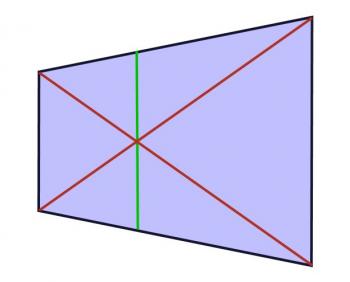
Is a calculator really necessary for this? Not at all! Most of these divisions can be built using construction lines that you erase later. For example, if you want to divide a plane surface in half, draw the two diagonals. Where they intersect is the point where the surface should be divided.

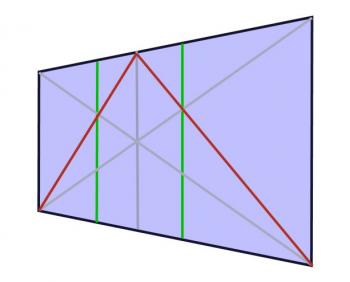
If you want to divide into thirds, it's a little trickier; one way is to do the two-way split, and then connect the corners to the opposite endpoint of the center line. The new intersection points are the three-way split.

And the constructions just get more and more ugly from there! So really, who wants to draw and then erase all those construction lines? Simply punch your lengths in, and get the result you need in seconds. Remember that the results are measured from the end of the horizontal segment that is closest to the vanishing point, as shown in the diagram above.

Doing the Math

The math involved in this calculator is based on the simple idea that as your traverse the plane from one end to the other, the regions are similar, and that the constant of proportionality is the same between each pair of successive regions. In other words, if the width of the first region is W, the next region's width is Wk (k being the proportion constant) and the next region's width is Wk(k) = Wk².

Knowing that the same proportion also applies to the heights allows us to calculate the constant k; multiplying the short vertical side by kⁿ gives us the longer side. Thus, L = Skⁿ, from which we conclude that k is the n^th root of L/S.

Now that we know k, we have the following: H = W + Wk + Wk² + ... + Wk^n-1. We can solve this for W, thus obtaining the width of the first region. We multiply each width by k to obtain the next one, and add the previous widths to get the distance from the vertex.

What about Divisions on the Vertical Axis?

Good question! This involves taking the n-sector of the angle between the horizontal pieces. This is not the same as doing an n-sector of the vertical side.

At some point soon we'll have a vertical version of this horizontal calculator. For vertical divisions, the artist will need to provide the length of the vertical segment, as well as the distances of the two endpoints from the vanishing point. Stay tuned for more details.