Hi Professor Puzzler. We learned in Calculus that if two functions are continuous, their sum is continuous. My teacher said that it doesn't work the other way - if the sum of two functions is continuous, that doesn't mean the two functions are continuous. She didn't give an example. Can you? Melinda, Arkansas

Hi Melinda,

The easiest way to give you a counter-example is using functions that are defined piecewise. Let f(x) = 1, when x > 0, and f(x) = 0 when x ≤ 0. Now let g(x) = 0 when x > 0, and g(x) = 1 when x ≤ 0,

The sum of these two functions is f(x) + g(x) = 1, for all values of x. This function is continuous, even though neither of the functions it was created from are continuous.

Here's another example: Let f(x) = [x] and g(x) = -[x]. Both of these are non-continuous functions (they are step functions), but when you add them, you get f(x) + g(x) = 0, which is also continuous.

As a matter of fact, if f(x) is any non-continuous function (but defined everywhere), doesn't it make sense that if g(x) = -f(x), the sum of the two functions would be continuous?

"I was told that when I'm rounding, if the number is less than 0.5, I round down, otherwise, I round up. But couldn't that mean more things rounding up than down, since 0.5 is right in the middle, and it gets rounded up?" ~ Quin from Chicago

Hi Quin, before I give you an answer, let me give an example of what you're talking about, to make sure all my readers understand your question.

Suppose you have 8 numbers: 4.1, 3.2, 2.5, 4.5, 5.5, 7.5, 1.6, and 4.9. There are just as many numbers with the tenths place below 0.5 as there are above 0.5, so you might expect that half of them round down, and half of them round up. But that's not what happens. Only two of them round down, and the other six found up. That seems very unbalanced.

Some people might wonder why that even matters. It matters if you have a lot of numbers and you're adding them together.

If you add all of the numbers above you get 33.8 But if you rounded them all, and then added them, you would end up with 36, which is a 6.5% error from the unrounded sum. Now, we don't expect the rounded sum to exactly match the unrounded sum, but this oddity that occurs when you have a bunch of numbers exactly at the midpoint of the rounding makes us wonder (as it made you wonder) if there might be a better way to do this.

It turns out there is an alternative method of rounding which is used in the circumstances described above:

• There are many numbers being added or averaged
• It's not unreasonable to expect that many of the data points will be exactly at the center mark 0.5

Under these circumstances, we can use the following rule for rounding:

If the decimal portion is less than 0.5, we round down, if the decimal portion is more than 0.5, we round up, and if the decimal portion is exactly 0.5, we look at the place value to the left of the five (yes, really, the left!). If it's an odd number, you round up, and if it's an even number, you round down.

For example, our four numbers above that end with a five would round as follows:

2.5 rounds to 2
4.5 rounds to 4
5.5 rounds to 6
7.5 rounds to 8

Another way of saying this is that we always round to the even number in the circumstance where the decimal is exactly 0.5.

So what happens if we do this? Our sum for the values given is 34, which is closer to the 33.8.

There's no guarantee that you won't end up with significant rounding discrepancy (if, by random chance, all your values were less than 0.5, your sum would be way off no matter how you round), but the odds of having large discrepancies decreases if you use this method.

The same method can be used at any place value. If you are rounding 135 to the nearest ten, it would be 140, but 125 would be 120.

Should you use this method of rounding? If you're a student, the answer is: only if your teacher tells you to do it this way!

"Sqr(2 + Sqr(3)) + Sqr(2 - Sqr(3)) works out to a simple radical (the square root of six). But not all radical expressions like that are so nice. How can you tell whether it'll simplify?" ~Paul

Hi Paul, whenever I have a question like this, I automatically think, "I'm going to replace the numbers with variables to see what happens."

So I'm going to rewrite your expression with variables, and then start manipulating it algebraically:

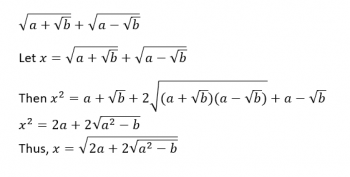
Eighth grader Gujjar wants to know, what is an "amount set aside for the poor and needy?"

Hi Gujjar, I'm guessing that you're looking for a specific word with that meaning? Probably the word you're looking for is "alms."

The word alms is defined by one dictionary as "charitable donations of money or goods to the poor or needy."

Notice that "alms" is a plural noun; it is defined as "donations" rather than "donation." However, I have never ever heard the word used singularly as "alm" - you wouldn't say "I gave an alm" for "I gave a gift to the poor." Even if it was just one gift, you would still say, "I gave alms."

Alms-giving is treated differently in different parts of the world. Here in the United States, if you're driving down a city street, it's not unusual to find a person standing at the corner with a sign asking for money. The tendency here is to not engage; we are often suspicious that the recipient might use the money for bad purposes (i.e. drugs). In one place I visited in north Africa, I remember being surprised at the number of people who were on street corners asking for money, but I was even more surprised at the number of people who engaged with them. It was explained to me that it is simply part of the culture, and people carry coins in their pockets specifically for the purpose of giving. In some religions, alms-giving is commanded, and in most religions it is strongly encouraged.

In his Sermon on the Mount, Jesus famously said, "Therefore when thou doest thine alms, do not sound a trumpet before thee, as the hypocrites do in the synagogues and in the streets, that they may have glory of men. Verily I say unto you, They have their reward. But when thou doest alms, let not thy left hand know what thy right hand doeth: That thine alms may be in secret: and thy Father which seeth in secret himself shall reward thee openly."

Jesus makes the assumption that people will give to the poor and needy*, and then points out that even something as good as giving to the poor can be undertaken badly; it is not done in order to receive glory from people. If you give in the hope that people will pat you on the back for your giving, you're doing it for the wrong reason. 

Instead, Jesus says, your giving should be so secret that even your left hand doesn't even realize that your right hand is being generous. That's a clever way of saying, "Keep it VERY secret" To this day, people still use the phrase "left hand doesn't know what the right hand is doing" - although most people use it to describe a situation where people are working at cross-purposes because they don't know what the other person is doing. But originally, it was meant as a positive thing, not negative.

Incidentally, in case "alms" wasn't the word you were looking for, here are thesaurus.com's synonyms:

aid, assistance, benefaction, charity, contribution, dole, donation, offering

[Note: the image shown above is a portion of a painting of Bishop Nicholas of Myra giving alms, painted by Jan Heinsch in the 1600s]

* It's no wonder that Jesus makes this assumption; the Old Testament has several commands and recommendations to this effect, such as in Deuteronomy 15:7 "If among you, one of your brothers should become poor, in any of your towns within your land that the Lord your God is giving you, you shall not harden your heart or shut your hand against your poor brother, but you shall open your hand to him and lend him sufficient for his need, whatever it may be." and Proverbs 19:17 "Whoever is generous to the poor lends to the Lord, and he will repay him for his deed."

"Hello The Professor. Please explain additive and subtractive in art." ~Anon

I'm assuming you mean additive and subtractive colors. This is a fascinating topic from both an artistic and a scientific point of view. 

Additive Color Sample

One of the best ways for me to help you visualize additive colors is to show you some color swatches generated on my computer. These color swatches will progress from left to right with the left-most swatch being fully saturated red, and then progressively adding more and more blue and green, until the blue and green are fully saturated in the last swatch. You can see that the swatches progress from red to pure white.

Subtractive Color Sample

For the subtractive color sample, I used my Prismacolor Premier Pencils. I made eight swatches in the following manner. I covered the entire region with my Crimson Red* pencil. Then I covered seven of the eight swatches with Copenhagen Blue and Grass Green. I then covered the entire region with red again, and colored six regions with blue and green. I repeated this process until my last layer of blue and green was just on the final square. The final result is that each swatch has eight layers of red, and successively from left to right they have 0, 1, 2, 3, 4, 5, 6, and 7 layers of blue and green. I've simulated the conditions of the additive sample, except using pigments instead of light.

As you can see (and I verified using a color-chooser tool in my graphics software) the last square is almost perfectly gray with just a hint of blue (it's very close to black - we would call it 85% cool gray).

What's the Difference?

One simple way of describing the difference is to say that in one case, light is emitted, and in the other, it is reflected. It should seem reasonable to you that if you add more light, you'll get something brighter, not something darker. 

My computer screen is emitting the light, rather than reflecting it.

But when you're dealing with pigment, you're not dealing with something that emits light; you're dealing with something that reflects light. My red pencil reflects red light. But wait! If it reflects red light, what does it do to all the other colors of light? It absorbs them. So white light (which is made up of all the colors) hits my red pencil, all the visible light except the red gets absorbed and doesn't reflect (in reality, the pencil is made up of pigment suspended in wax, so it is somewhat translucent; some of the light passes through the wax and pigment, hits the white paper, and is reflected back).

Of course, the same is true of the blue and green; the blue pencil absorbs everything except blue light, which it reflects, and the green pencil absorbs everything except green. So what happens when I put a layer of red, a layer of blue, and a layer of green down on paper? Each of the three colors is partly absorbed by the other two pigments, which deadens the color. Keep adding more layers, and you decrease the translucence, and the color gets more and more "dead and dark." Why is it called "subtractive"? Because more and more light is absorbed, which decreases the amount of light that is reflected.

* I've included Amazon links to the individual colors so you can see what they look like, but I don't really recommend buying individual pencils from Amazon. You'll get a good deal on a set from Amazon, but when it comes to buying individual pencils (which you will do on a regular basis - you'll find there are certain colors you just love using, and you can't get enough of them), you'll want to visit your local art store (and I don't necessarily mean the big name chains like Hobby Lobby) and see what their prices are. If you are fortunate to have a locally owned art store, consider supporting them with your business. If you spend some time getting to know the people that run them, you may feel comfortable asking them questions about their business. You may find that they take a loss on some items in order to get people in the store. Find out where they make their money (it's probably scanning and framing of artwork), and take that business to them.