Yesterday we received the following question: "What is estimating?"

This is a fairly broad question, but it's worth answering.  I'll explain briefly what it is, and then after that I'll talk about why it's important to be able to estimate.

The following is a screen shot from our game "Guess It!" in the Junior section of the site.

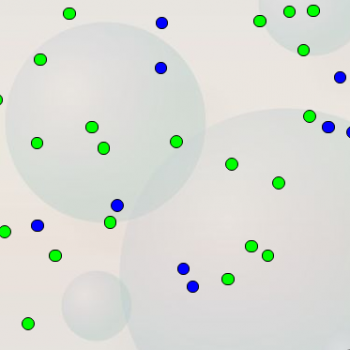
When you are playing "Guess It," the site might ask you a question like "Are there more green dots or blue dots?" You will automatically say, "There are more green than blue." But how do you know? Did you stop to count all the green dots, and then count all the blue dots? Hopefully you didn't! Hopefully you were able to quickly scan the image and recognize that there are more green, without taking the time to count them. That's estimating.

The site might ask you "Is the number of green dots closer to 10 or 50?" Do you need to actually count the green dots in order to answer the question? No!  You've probably got a good sense for what a group of ten dots would look like, and it's fairly obvious that the image doesn't contain 5 groups like that. So you would say "It's closer to 10 than 50!" That's estimating.

Estimating is when we don't need to have an exact answer; we just want to be "in the ballpark."

Why Is It Important?

Suppose you had $50.00 in your wallet, and you went grocery shopping. You don't have a calculator with you, and you don't want to add all your purchase prices by hand, but you want to be sure you don't get to the cashier with a cart full of items that add to more than $50. Your items cost $7.96, $3.20, $13.84, and $4.42. You can do some estimating like this: "I'll round all my items up to the next multiple of five so I can add them easily. If the sum is less than 50, then I know I'm okay. $10, $5, $15, $5. 10 + 5 + 15 + 5 = 35, so I'm okay!"

Estimation is also a great way of checking to see if your conclusions are reasonable. If I'm trying to calculate how long it will take an object to fall to the ground from the roof of my house (yeah, I calculate silly stuff like that, because I'm a Physics teacher!), I can mentally picture it falling, and estimate: "Well, it certainly won't take more than 5 seconds!" and so if I do my calculations and come up with an answer of 35 seconds, I know something must be wrong!

I do a lot of estimating while I'm teaching. Using the "falling to the ground" example above, I know that the acceleration due to gravity is 9.8 m/s², which is not a nice number to work with if you don't have a calculator. But it's really close to 10, so if I'm doing a freefall problem on the board, and don't want to pick up a calculator, I'll do an estimation by replacing 9.8 with 10, and work out an approximate answer in my head. Then, when my students start telling me the numbers they came up with, I'll ask myself, "Is that reasonably close to my answer?" If it is, I'll feel confident that they got the answer correct.

In general, I find that my students who are good at estimation do much better than the ones who do not, because they are quicker to recognize whether their answers even make sense! That's not just a good thing in school; it's a skill that will transfer to your job and your every-day life.

Here's a common question among math teachers and students (and math dabblers who just like to raise people's hackles!):

"If you see 3/2x, how do you interpret it? Is it 3 divided by 2x? Or 3 divided by 2, times x? Order of operations says we do division and multiplication left-to-right, which leads to the second answer. However, if you look at the slash as a division symbol, it appears to be the other way: 3 is the numerator and 2x is the denominator."

The correct answer to this question is: it's neither.

That's right. It's neither 3/(2x) nor 3/2 times x.

So no matter which way you were arguing, you're wrong. Let me explain.

Whenever you come across something like this: 3/2, the standard reading is not "three divided by two." You read it as "three over two," (this is considered to be the proper designation for the slash symbol when used in this context). This lends credence to the notion that the slash is being used as a fraction bar, and therefore, our example should be read as a fraction: 3/(2x).

But did you know that there are specific rules for how you write fractions using standard typographic practices? First, you are expected to use a specific slash symbol, which is not your standard "forward slash" on your keyboard - it's a unicode symbol called "fraction slash." The fraction slash is designed with minimal kerning (space between characters), and there's a very good reason for this.

There's another typographical practice we must follow: we superscript the numerator and subscript the denominator. The superscripts and subscripts, combined with the minimal kerning, result in the numerator being above the slash, and the denominator below.

Thus, we would either write: ³/_2x or ³/₂x, and now you can see that proper typographic practices makes it clear which way we intended it to be interpreted.

In other words, 3/2x is actually just a typographical error, and not a real mathematical expression. It's the result of someone being lazy. (Don't worry, I've done it too!). With the sophisticated word processors we have these days, with powerful equation editors, there's no longer any excuse for any mathematician to type 3/2x. In fact, with equation editors, you can get expressions that appear much nicer than the ones that you create with superscripts and subscripts.

Of course, there is one place where this typographical error still shows up: calculators.

Many calculators are not designed for proper typographical display of fractions. So what do we do? We do one of the following:

1. Figure out which way your particular calculator handles this expression, and always do it that way.
2. The safer approach: When dealing with a calculator, always clarify your meaning by including parentheses.

Once you've settled on one of these practices, it's time to accept the fact that you haven't been arguing about some standard of mathematics, but about typography.  It's now time to do some real math, and leave behind the arguments about typographical quirks!

Professor Puzzler

Sixth grader Elise asks, "I don't get BODMAS. Can you help me?"

Well, Elise, this is one of my favorite questions, and I get asked this a lot. But I've never written it up on the "Ask Professor Puzzler" blog, so here we go!

Before I get started explaining BODMAS, I need to mention that in different parts of the world, this "rule" is known by different names. You call it BODMAS, but some people call it PEMDAS. So when I explain what it means, in parentheses I'll explain what it means to people who call it something different.

The six letters each stand for something you can do to combine numbers in mathematics:

B = Brackets (P = Parentheses)
O = Order (E = Exponents)
D = Division
M = Multiplication
A = Addition
S = Subtraction

These six letters indicate the order in which you do the operations in a mathematical expression. For example, if you see the following:

2 - (3 + 2),

You notice that "3 + 2" is in brackets (parentheses), so you do that FIRST: 3 + 2 = 5

Now you have 

2 - 5 = -3

Why does it matter which order you do things? It matters because you would get a different answer if you did the subtraction first:

2 - 3 = -1

-1 + 2 = 1

Uh oh! One way we get -3, and the other way we get 1!

Here's another example. Suppose you have 1 + 2^3 (1 + 2 cubed). If you did that from left to right, you would add 1 + 2 and get 3. Then you would cube that and get 27.

But what you're SUPPOSED to do, is evaluate the exponent first: 2 cubed is 8. Then you add 1 + 8, and get 9. It all depends on what order you do things, so you have to get the order right!

You see, we have to have an order of operations, or nobody would ever calculate expressions the same way. Order of Operations is a rule that helps to make sure EVERYONE evaluates the same expression in exactly the same way.  If we didn't have order of operations, people would get different answers for the same problem, and that would be horrible - nothing would ever get done, and none of our technology would work right because teams of engineers would always be fighting over how to evaluate the equations and formulas they work with, and if they didn't use proper order of operations, not only would things not work right, you could end up with some pretty horrible catastrophes (imagine engineers using heat formulas in nuclear reactors or power plants, and not calculating correctly how much cooling they need!).

Now here's the tricky part (and I've even had emails from MATH TEACHERS who don't understand this part!): you DON'T do all your multiplication before all your division, and you DON'T do all your addition before all your subtraction. Multiplication and division are on the same order of priority, and addition and subtraction are on the same order of priority. If a problem has both multiplication and division operations, you do them from left to right. If a problem has both addition and subtraction, you do them from left to right as well.

So really, it should be written BO (DM) (AS)* to remind you that division and multiplication go together, and addition and subtraction go together.

* Or PE (MD) (AS)

If you want some practice using BODMAS (PEMDAS), you can try our One To Ten Game, which challenges you to put toghether expressions that add up to all the numbers from one to ten.

It's been showing up in social media - on August 27th, 2015, there will be an amazing sight in the night sky; there will be a double moon! Why? Because Mars will appear as big as the moon on that day.

True? Or hoax?

Professor Puzzler says: HOAX!

Take a look at the image below to get a better idea of how crazy that would be:

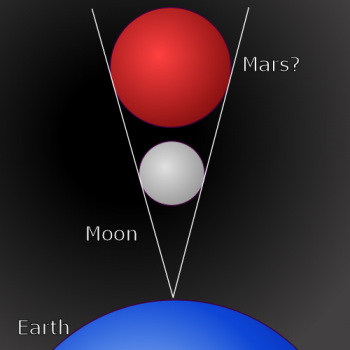
In the picture you can see (roughly) the scaled sizes of Mars and the moon. Surprisingly, mars is only twice as big in diameter as the moon. (The distances are not on the same scale as the sizes, since that would result in a picture with a cone almost too narrow to see.)

In order for Mars to appear the same size as the moon, it needs to fit snugly inside the visual cone with apex on the surface of planet earth (where you're standing, looking into the night sky).

We could draw some similar triangles connecting the apex, the tangents to the two bodies, and the centers of the two bodies; since these are similar triangles, they have to have the same side ratios. What does that mean? It means that if the radii are in the ratio 1:2, the distances have to be in the ratio 1:2.

In other words, Mars would be about 500,000 miles from planet earth. Since, at its very closest, Mars is about 30 million miles from planet earth, Mars is going to somehow have to teleport itself a few million miles out of its orbit to appear that big to us on its one-night engagement as the moon's twin brother.

Of course, this sudden, dramatic appearance of a new celestial body in our orbit is going to cause some pretty drastic effects, including - I would imagine - significant tidal forces, volcanic eruptions, and earth quakes.

Let's hope this isn't going to actually happen!

[And presumably, after its one night visit, Mars is going to somehow teleport itself back, which will result in more gravitational disturbances the next day!]

Jim writes: "I have included "My Secret Word" as a daily game for those in my private Facebook Group We play the game and post our scores and the last player each day posts the word when he or she solves he puzzle. Lately, when I follow the posted link address I do not get the same game as the others. Why is that? How can I fix that? Please help."

Jim, I actually sent you a reply email, but it got returned with a "mailbox unavaiable" message, so I'm posting my reply here, in hopes that you'll see it!