Dave, an 8^th grader, asks:

Let's say you are making a list. Would you, or would you not put a comma before the “and”?

Good question. What Dave is referring to here is the Oxford comma, sometimes also called the “serial comma.” We know that we should put a comma between each item in a list to avoid confusion, but there is some debate over whether there should be a comma after the second-to-last item.

For example:

“Today we went to the store and bought milk, bread, eggs, and apples.”

The comma after the word “eggs” is an example of the Oxford comma. Some say that this is unnecessary, because the word “and” indicates the almost-end of the list and serves the same function as a comma.

Those opposed to the Oxford comma would write that sentence this way:

“Today we went to the store and bought milk, bread, eggs and apples.”

Now, the addition of an Oxford comma may not seem like a big deal in a short sentence like this. But the longer the sentence gets, the more useful it can be. And I don’t mean “longer” in the sense of more items in the list, but more complex “items,” such as phrases rather than single words.

For example:

“When interviewing potential new employees, Richard was careful to pay attention to each candidate’s sense of confidence in their abilities, attitude toward their previous education and employment and their ability to express themselves in a succinct manner.”

That’s a pretty long sentence, and each item is much longer than in our previous sentences. Do you see how the section “education and employment and their ability” could be confusing upon first reading? Without the Oxford comma here, that last segment is a lot longer and starts to feel like a run-on sentence.

 Let’s look at this sentence again with the Oxford comma:

“When interviewing potential new employees, Richard was careful to pay attention to each candidate’s sense of confidence in their abilities, attitude toward their previous education and employment, and their ability to express themselves in a succinct manner.”

By using the Oxford comma, we help to avoid confusion about whether the word “and” is being used as a part of one of the list items, or indicating the last item of the list.

Those who recommend the use of the Oxford comma will also use sentences similar to the following one, as an example for why we need that extra comma:

“I’m grateful to my sisters, Jan and Devon.”

What is the speaker saying here? Are they grateful for their two sisters who are named Jan and Devon, or are they grateful to their sisters and two other people named Jan and Devon? In other words, does the comma introduce the first item in a list, or does it introduce an elaboration upon that first item?

So that's an explanation of the Oxford comma.

But that’s not what this question is asking. The question is asking whether the Oxford comma should be used in general.

Well, first I’ll tell you what a couple style guides recommend.

The Chicago Manual of Style says the following:

“When a conjunction joins the last two elements in a series of three or more, a comma—known as the serial or series comma or the Oxford comma—should appear before the conjunction. Chicago strongly recommends this widely practiced usage … since it prevents ambiguity.” (6.18)

The AP Stylebook, on the other hand, says to omit the Oxford comma in a simple series, but recommends it for a longer, more complex series (like the second pair of sentence examples above).

Personally, I use the Oxford comma even in a simple series, following Chicago’s recommendation. For one thing, consistency is important, and rather than trying to determine how “complex” a complex sentence must be before it merits a serial comma, I think it’s best to use it in every series. When we are able to expect the Oxford comma to be used, we don’t have to wonder while reading whether an “and” is a conclusion of a series or part of a series element. (For example, “For breakfast we had eggs, bacon, toast and jam.” One might expect “toast and jam” to be a combined element, and so without the Oxford comma, you have to finish the sentence before you figure out what the “and” is doing.)

The role of punctuation is to make our words easy to understand, and having the consistent structure of an Oxford comma in place aids in understanding. The more consistent we can be with punctuation, the more attention we can focus on the words themselves, and the more quickly and easily we’ll be able to read and understand another’s writing.

Hi Professor, I saw this riddle on a website: "The sum of three numbers is equal to their product. What are the numbers?" They gave an answer of "1,2, and 3". I wondered if this is the only answer. verity

Hi Verity,

In order to answer this question, we should start by writing the problem algebraically:

abc = a + b + c

What you should notice right away is that there are three unknowns (three variables) and only one equation. This makes it seem very likely that there will be multiple solutions. The first thing I tried with this equation was to solve for one variable. Shall we solve for a? Here are my steps:

abc = a + b + c 
abc - a = b + c  (subtract a from both sides)
a(bc - 1) = b + c (factor out an a)
a = ^{(b + c)}/_{(bc - 1)} (divide both sides by bc - 1)

You know what this looks like to me? It looks like we can pick any values we want for b and c, as long as b and c aren't reciprocals of each other, and we'll get a value for a. b and c can't be reciprocals of each other because then (bc - 1) would be zero, and we'd have a division by zero, which is illegal, immoral and socially unacceptable.

So let's pick a couple values. b = 3; c = 4.

a = ^{(3 + 4)}/_{(12 -1 )} = ⁷/₁₁.

Let's test our answer:

3 + 4 + ⁷/₁₁ = ⁸⁴/₁₁.

3(4)(⁷/₁₁) = ⁸⁴/₁₁.

Sure enough, they're the same! So the answer to your question is, no, their solution is not the only one; there are an infinite number of solutions.

I suspect that the site intended to make it more challenging by requiring you to use only integers, or maybe distinct integers. But that doesn't change the fact that there's an infinite number of solutions. For any integer x, the following three numbers work:

x, 0, -x

Someone told me that "most people have a higher than average number of bones in their body." That doesn't even make sense to me. How can most people be above the average?

Whoever told you that is probably not right, but I'm pretty sure I know what they were reasoning. So first I'll explore their reasoning, and then I'll present an alternate view of the statement.

You see, the 'normal" human has 206 bones in their body, but the average number of bones in the human body, if you were to take a survey of all humans currently alive in the world - is slightly less than 206.

Why? Because some people were born without arms or legs. Others have had limbs amputated. So if you average the number of bones of all the people in the world, you'll end up with a number slightly lower than 206.

Let's just make up some numbers, so you can see what I mean.

We'll say that the population of planet earth is 8 billion people. Of these 8 billion people, we'll hypothesize that 0.5% of them have lost a limb (rough estimate based on the number of people in the U.S.A. with amputations), and that limb loss has cost them 30 bones (I'm completely making that number up).

So we have 7,960,000,000 people with 206 bones, and 40,000,000 people with 176 bones. How many bones is that in total?

7,960,000,000(206) + 40,000,000(176) = 1,646,800,000,000

That's a lot of bones! So to find the average number of bones per person, we divide by our 8 billion figure: 205.85.

Since most people have more than 205.85 bones, most people have a higher than average number of bones in their body.

Okay, so that's the reasoning your friend was using. But it's not quite right. Because, you see, when you are born you have about 300 bones in your body. These bones are connected by cartilage, and will eventually fuse together (the process by which cartilage turns to bone is called "ossification"). How long does it take this process to complete? Well, I don't know for sure. One site I looked at said the process is complete around the age of 20, another said 25. I didn't feel like tracking down more research on that, so let's go with the smaller number, and say the process is done at age 20.

This is important: I'm attempting to prove your friend wrong, which means that at every step, my rounding is going to be done in the direction that favors your friend's hypothesis. Because if he's wrong in the best-case scenario, then we know he's wrong for sure!

Now, I have no idea how many bones a child has at various ages, so here's what I'm going to do. I'm going to assume the best case scenario - every child under the age of 20 has 1 extra bone, leading to a huge chunk of the population having 207 bones instead of 206. Again, I know that I'm lowballing this massively, but my goal is to give your friend's hypothesis the benefit of the doubt.

So now we have to rework our numbers, and for this, I'm going to use 25% as the percentage of people in the world under the age of 20. This number is not completely out of my hat - I based it on some numbers for U.S.A. population, and rounded down a bit. 

In our previous calculations, we had 1,646,800,000,000 bones, but now I want to break it down by adult vs. child, so I'm going to multiply that by 0.75 (75%) to get the number of adult bones:

Adult bones = 1,646,800,000,000(0.75) = 1,235,100,000,000

For children's bones, we'll take the total in our previous calculation and multiply it by 0.25 (25%). However, this number is based on 206 bones per person, so we're going to then divide by 206 and multiply by 207. This number isn't going to come out even, so we'll round down, in fairness to your friend's hypothesis.

Child bones = 1,646,800,000,000(0.25)(207)/206 = 413,700,000,000.

Now let's add the adult bones and child bones together: 1,648,800,000,000. This is only slightly larger than the other number we obtained (because I did so much rounding down), but it's enough to put us on the other side of 206:

1,648,800,000,000/8,000,000,000 = 206.1

So it turns out that most people (the adults without amputated limbs) have a below average number of bones. Bear in mind that some of these numbers I pulled out of a hat without a lot of research, but I think it's safe to say I lowballed enough numbers that we can be reasonably sure of the conclusion. If you disagree, drop me a note with your reasoning!

First of all, I want to make it abundantly clear that this post is not political in nature. It is not an attempt to endorse one candidate, or repudiate another candidate. It is, pure and simple, pointing out how easy it is to misuse mathematics and statistics to try to emphasize a point. Take a look at this image, which is floating around on facebook.

What is the intent of this picture? Well, looking at the caption under the photo, which read, "Who speaks for you? Bernie Sanders 2016," makes it clear that the intent was to show Sanders as a "man of the people" and the rest of them so insanely rich that they are out of touch with the American people.

But the reality is distorted by the image's choice of mathematical language. Specifically, the choice was made to use the text "¾ million" when referring to Cruz's home, instead of the text "750 Thousand." This, I am certain, was deliberate. Because "milllion" sounds massive compared to "thousand," and if they had written "750 Thousand" next to Cruz, people would be much more likely to realize that Cruz is in the same ballpark with Sanders, and not in the same ballpark as Trump, or even Clinton.

To those who are reading quickly, or who didn't do well in math, "¾ million" sounds much larger than "750 thousand," even though the two phrases are expressing exactly the same value.

In mathematical terms, instead of talking about "ballparks" we talk about "orders of magnitude." Two numbers have the same order of magnitude if the larger one divided by the small one is less than 10.

And guess what! Cruz and Sanders have the same order of magnitude. Would you like to see a graph of these values? Here it is:

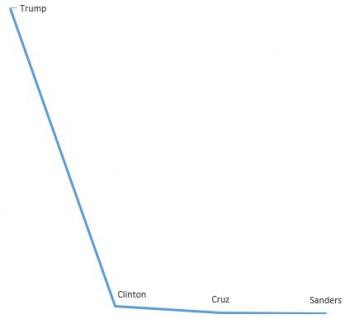
Notice that compared to Trump, Clinton's homes seem inexpensive, but compared to both of them, Cruz and Sanders are downright indistinguishable*.

Do I care how rich these guys are? Not even a whit. I have no problem with a rich president. I have no problem with a middle class president. I have no problem with a poor president.

I have a problem with people using mathematics to deceive the people who do care about such things. A good piece of advice for you when looking at a set of statistics: take note of all the units given (in this case, "millions" was given as the units throughout, until the very end) and if the units are not consistent throughout, ask yourself why. It may be that there's a good reason, but it could very well be (as in this case) that someone is trying to fool you. To keep things consistent, the graphic creator should either have written the Cruz value as "750 Thousand" or the Sanders value as "3/10 Million."

The person responsible for the graphic probably was hoping for one of the following:

1. You slept through the math lessons where your teacher taught you about place value and magnitude.
2. You'll be in such a hurry to click "like" that you won't take a moment to remember the lessons you learned.

After all, it's an election year. What did you expect?

* You might be thinking to yourself, "You really think that the difference between a 300 thousand dollar home and a 750 thousand dollar home is not significant?" And if that's what you're thinking, you're sort of missing the point here. The point is that the person who made the graphic was afraid that if he represented the facts in an honest manner, you would think it was an insignificant difference, and so he chose a dishonest path, hoping that your gullibility would do the rest. 

I was told that the number 1,000,001, no matter what base you're working in, is a composite number. Is this true?

Hmm...that's an interesting question. Let's look at some sample bases to make sure it's a reasonable statement.

If this was base ten, then we'd have 1,000,001 is divisible by 101, so it's composite.

If this was base eleven, then the number would be equal to 1,771,562 (base ten), which is obviously composite, because it's even!

Actually, now that I think about it, any time the base is an odd number, 1,000,001 represents an even number, so it's definitely true for all odd bases. So let's focus on even numbered bases.

Let's try base eight. This number would be equal to 262,145 (base ten), which is a multiple of 5.

Base six? That's 46,657 (base ten), which is divisible by 37.

Now, I could keep trying more bases, but I just noticed something interesting. In our first example, the number is divisible by 101, which is one more than the square of 10, and in our last example, 46,657 is divisible by one more than the square of six. That's interesting. Your number may always be divisible by one more than the square of the base. Let's test that hypothesis.

In base twelve, this number would be 2,985,985, and if our hypothesis is correct, it will be divisible by 12² + 1, or 145. Pull out your calculator...

It is!

So we have a reasonable extension of your conjecture: If 1,000,001 is a number written in base n, then it is divisible by n² + 1.

Ideally, it would be nice if we could prove this extension, because if we could, we'd be closer to proving your conjecture.

Let's write our number 1,000,0001 in terms of the base n:

1,000,0001 = 1·n⁶ + 1.

And suddenly I'm remembering one of my factoring rules - the rule for a sum of cubes:

n⁶ + 1 = (n²)³ + 1³ = (n² + 1)(n⁴ - n² + 1)

Sure enough, 1,000,0001 will always be divisible by one n² + 1!

So in order to finish proving your conjecture, we simply need to show that (n² + 1) can't be equal to 1, and it can't be equal to n. These are the two circumstances which could result in  n⁶ + 1 being prime (a number is composite if it has factor pairs other than one and itself).

n² + 1 = 1 has only one solution: n = 0. But we don't work in base zero, so this is irrelevant.

n² + 1 = n, or n² - n + 1 = 0, which has no real solutions, so YES! The conjecture we started with is true!

Thanks for asking - that was an interesting exercise!
Professor Puzzler