After school one day last week, one of my students wanted a little help with some problems she was working on. One of the problems was a system of two equations in two unknowns:

x² + xy = 30
xy + y² = 6

I said to her, "I like problems like this. I don't know right off the top of my head the best way to start it, and that means it's an interesting problem!" I asked her what she had tried.

She said, "I multiplied the second equation by -1, and then I added it to the first equation, to get rid of the xy term."

x² + xy = 30
-xy - y² = -6

------------------

x² - y² = 24

"That's good," I said. "So what next?"

"I don't know," she said, "that didn't seem to get me anywhere."

I said, "Okay, well, let's leave that there; we may want it later." So I put a box around it, to make sure I wouldn't erase it from the board. "Did you try anything else?"

"I couldn't think of anything else to try."

"Did you try adding the equations?"

"But nothing will cancel if I do that..."

"Try it anyway. I think something interesting will happen. I'm not sure it'll be USEFUL, but it'll at least be interesting," I said.

We did the equation addition:

x² + xy = 30
xy + y² = 6

------------------

x² + 2xy + y² = 36

It didn't take her long to notice that the left side could be factored:

(x + y)² = 36

"And what does that tell us?" I asked.

"x plus y is either 6 or -6." 

"That's great," I said, "you've just turned this into two problems!" So I drew a chart showing the two choices:

Choice One: x + y = 6

Choice Two: x + y = -6

"Now, I said," let's go back to your first equation that you came up with. Can you think of anything you can do with it?"

She realized she could factor the left hand side:

x² - y² = 24 ⇒ (x - y)(x + y) = 24

At this point she was getting a little excited about the problem, because it was starting to fall apart quite nicely. After all, if x + y = 6, then  (x - y)(x + y) = 24 is equivalent to (x - y)(6) = 24, or x - y = 4. Similarly, if x + y = -6, then (x - y)(-6) = 24, or x - y = -4.

Now we find that we have two systems of equations:

Choice One: x + y = 6 and x - y = 4

Choice Two: x + y = -6 and x - y = -4

Both of these systems can be quickly solved (my student did them both in her head), to obtain the solutions (5, 1) and (-5, -1).

And the best part of my teaching day was hearing these words: "That was FUN!"

Then I showed her how the Teacher's Manual suggested doing the problem. Solve one of the equations for a variable:

x = (6 - y²)/y, and then substitute that into the second equation. I showed her the full solution. It was UGLY.

"I like our method better! Ours was fun!"

I understand the reasons for teaching the method that's in the text book; it's straightforward (even though it's ugly), and will work on a variety of problems. In addition, using that method gives students practice on a few different topics such as fractions and squaring binomials, etc.

We had no guarantee, when we first started the problem, that our ideas of subtracting and adding the equations were going to get us anywhere useful. As I said to the student, "We might try a bunch of things before we find something that works, but sooner or later we'll hopefully stumble on something useful."

But that's what problem solving is. Problem solving is not just using a rote method that a textbook shows you. It's looking at a problem and not knowing where to go, but being willing to try things to see what will happen. It's adding two equations together because you notice that adding them creates a perfect square, and that might be useful. It's subtracting two equations because you notice that it eliminates an xy, and that might be useful too.

It's a labyrinth of possibilities, with no guarantee that the things you try will be useful, but with the hope that somewhere there's a path that leads to a solution.

And, in the end, it's the delight of watching a system of quadratic equations disintegrate into pieces that you can solve in your head. It's the spark of excitement when the solution starts to dawn in a student's mind.

And it can be FUN!

Someone told me that on the Richter Scale for earthquakes, adding 1 gives an earthquake 10 times as big. Question 1: is this true?

Then they told me that adding 0.5 does not give an earthquake 5 times as big. Question 2: is that true, and why?

Doreen

Hi Doreen,

To both of your questions, the answer is "Yes."

The Richter Scale is called a "logarithmic" scale, which - for our purposes - just means that a 4.0 earthquake is 10 times as "big" as a 3.0 earthquake. And if you go from a 4.0 earthquake to a 6.0 earthquake, that's an earthquake 100 times as big (multiply by 10 to get to 5.0, and multiply by 10 again to get to 6.0).

("bigness" of an earthquake has to do with the amplitude of its seismic waves).

Regarding your second question, it is tempting to think that if a change of 1 means "ten times as big," a change of 0.5 means "five times as big." But it doesn't work that way.

Let me show you why. Let's talk about a 3.0 earthquake, a 3.5 earthquake, and a 4.0 earthquake.

You know that if you go from a 3.0 earthquake to a 4.0 earthquake, that's 10 times as big.

But if a change of 0.5 meant 5 times as big, then we'd calculate:

From 3.0 to 3.5 is 5 times as big;
From 3.5 to 4.0 is 5 times as big;
Therefore, from 3.0 to 4.0 is  5x5 = 25 times as big! That's not right!

So let's just break down the math a bit.

If you want to go from a Richter scale reading of x to a Richter scale reading of y, you would take the difference of x and y, raise 10 to that number, and that's your "bigness" ratio.

For example, if you wanted to go from 2.0 to 7.0, your ratio is 10^7-2 = 10⁵ = 100,000.

So let's talk about a Richter Scale difference of 0.5:

Suppose you wanted to go from 2.0 to 2.5. Your ratio is 10^{2.5 - 2} = 10^0.5. What is 10^0.5? It's the square root of 10, which is approximately 3.1623.

So if one earthquake has a Richter value of 4.0, and another had a Richter value of 4.5, the 4.5 earthquake is 3.1623 times as big as the 4.0 earthquake.

By the same reasoning, we could figure out how much bigger a 4.2 earthquake is compared to a 4.1 earthquake:

10^{4.2 - 4.1} = 10^0.1 = 1.2589.

Vipin sends us the following question:

_+_+_+80+90=100 , no negetive number in the question.

There are multiple ways to solve this equation, but I have no idea if the ones I came up with are the ones the problem creator was looking for. That's okay. If you come up with a solution that works, it doesn't matter if it's "the right one."

For people reading this question, I'm about to propose a solution, so if you want to try to figure out a solution for yourself, do it now, before you read any further!

--- SOLUTIONS BELOW ---

The first thing I did to this was, I subtracted 80 and 90 from both sides of the equation, which turned it into:

_ + _ + _ = 100 - 80 - 90

_ + _ + _ = -70

If you don't mind, I'm going to replace those blanks with variables, because then I can talk about each individual blank by name:

a + b + c = -70, where a, b, and c are not negative.

I came up with a few possibilities; the first two use complex numbers.

Solution One

a = 0, b = -30 + i, c = -40 - i

I know, you'll be tempted to say, "Wait! -30 and -40 are negative numbers!" To which I reply, "No, -30 is part of the complex number -30 + i. Complex numbers are neither negative nor positive, so I have filled the blanks with numbers which are not negative."

Maybe you'd like to argue that the point is to not use the negative symbol at all. In which case, I give you solution #2:

Solution Two

a = 0, b = 30i², c = 40i²

I've used no negative symbols, but b and c evaluate to -30 and -40 respectively, giving the desired result.

Maybe you'd like to argue that you can't use negative symbols and you can't use expressions that evaluate to negative numbers. In which case, I would say, "Stop adding to the rules and find your own solution!" ;)

If you're willing to accept solution two, it opens up a boatload of possibilities, like using trig, or other functions:

Trig Solution

a = 0, b = 0, c = 70cos(180º)

If our readers aren't willing to accept any of these answers, please use the "Ask Professor Puzzler" link at the bottom of the page to suggest your own solution. Be sure to mention what blog post you're writing about! If we get any solutions we like, we'll add them to the bottom of the post.

One of my friends shared the following picture on Facebook this morning. He didn't specifically ask me for an answer, but I thought it would be a fun question to explore.

So let's start by asking a question: If it wasn't zero degrees, how would you figure out "twice as cold?" Did you say, "Multiply the temperature by two?"

So, for example, if the temperature was -10 degrees, twice as cold would be -20 degrees?

That seems like it might be a reasonable answer at first glance, except it clearly doesn't work that way, if you just ask this:

If the temperature was 40 degrees, what is twice as cold as that? Now multiply 40 by 2 and you get 80 degrees, which is clearly not colder!

So multiplying the temperature by two doesn't do what we want.

In addition to this, we have another issue with the question: temperature doesn't measure cold. It measures heat. In the same way that we don't measure darkness; we measure light. Amount of light is measured in lumens, and darkness is the absence of light. Cold is not a measured quantity; it is the absence of heat. So saying "twice as cold" may not have any actual meaning to begin with!

The next question to consider is: what scale are you using? Fahrenheit? Celsius? Because that must make a difference too. 0 degrees Celsius is the same as 32 degrees Fahrenheit, and multiplying the first number by 2 gives you zero, while multiplying the second number by 2 gives 64!

Having asked those questions, let's take a break from temperatures and talk about marketing and sales.

I know, I know, that has nothing to do with temperature. Bear with me, though, because I'll get back to temperature in a minute.

Suppose I was hired by a firm to do marketing and sales work. I was hired at the beginning of 2015, and at the end of the year, I wanted to impress my bosses with how much I'd helped the company's bottom line. So I show my boss this chart:

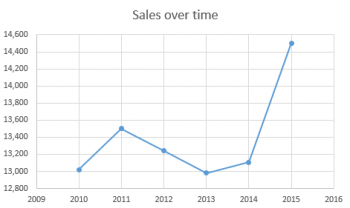
It looks pretty impressive, doesn't it? My boss, if he's not paying attention, will say, "Wow! Look at how much higher the 2015 number is! You've quadrupled our sales, just in one year!"

But if he's paying attention carefully, he'll say, "Wait a minute! Why does your chart's axis start at $12,800 instead of $0?

And the answer is...if my chart started at zero, my bosses wouldn't be nearly as impressed with me:

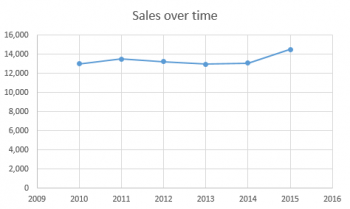
You see, once we have a frame of reference for comparison, we realize that the difference between the 2015 number and the 2014 number isn't nearly as big as it looked in the first chart. And I certainly didn't quadruple their sales, even though it looked like it in the first chart.

The same is true with temperatures: if you want to make comparisons like "twice" or "half," you really need to have a "real" zero. Zero on the Celsius scale doesn't actually "mean" zero, because zero should mean "no heat at all" (just like zero on my sales chart means "no sales at all"). We need to have a scale in which zero really means "no heat whatsoever."

Fortunately, we have a scale like that. It's the Kelvin scale, in which zero is called "absolute zero" because it is the end of the line. There is no heat whatsoever at zero Kelvin. In the Kelvin scale, 0 Kelvin is equal to -273.16 degrees Celsius, and 273.16 Kelvin is equal to 0 degrees Celsius.

Okay, so now let's make some assumptions. Let's suppose that the guy in the picture means 0 degrees Celsius. Let's also suppose that when he says "twice as cold" he really means "half as much heat energy."

If we make those two assumptions, then we can do the following:

0 degrees Celsius = 273.16 Kelvin

Half of 273.16 Kelvin is 136.58 Kelvin

And 136.58 Kelvin is equal to -136.58 degrees Celsius.

There ya go. If the temperature is 0 (assuming Celsius scale), and it's going to be twice as cold tomorrow, it'll be -136.58 degrees Celsius tomorrow. Of course, we had to make some assumptions along the way, but at least we have an answer!

Eighth grader Neha, from New Delhi asks the following question: "I want a set of maths questions of any level with solutions for my holiday homework."

Well, Neha, I'm always happy to see students wanting to do math while on holiday, so I'll make a couple suggestions for you. Of course, I don't know what you've studied, so it's tough to guess what kind of problems you want, but we have a lot of math problems on this site.

You may have noticed our "Pro Problems" section, which is quite large, and getting larger all the time. There are both math and physics problems there, and the math problems cover subjects from basic algebra through pre-calculus topics. Of course, this isn't what you're looking for, because these problems don't have solutions publicly displayed. Those problems are designed for teachers to assign to students, so solutions are only available to teachers.

So instead, if you want to see solutions as well, you can try this page: Maine Association of Math Leagues Problems. These problems were written over the course of several years to help some math competitors get ready for competitions. Some of the problems were written by me, and some of them were written by Sasha, a young man who did exceptionally well in those math competitions.

If you're looking for a harder challenge, you might try Graeme's High School Math Problems, Graeme wrote some very creative and quite challenging problems for this site, over the course of several years.

In these sections, the solutions can be displayed, so you can check your work. Each problem has a clear explanation, not just an answer.

I hope you have fun with your "holiday math!"