"I keep hearing about people who are good at math and music. But that seems so strange -- music is so artistic and flowery, while math is so technical and straightforward. How could either have anything in common with the other?" ~ Laura from Maine

Hi Laura, thanks for thre great question. I wish I could give you a solid scientific answer to this question, but the inner workings of the brain definitely are not in my field of study. Instead, I can give you some observations about both math and music, based on my own experiences as a mathematician and a musician.

First, I can confirm that what you said is typical in my experience - it is very common for people who are good at music to also be good at math (and vice-versa). Obviously, that's not a 100% rule (probably not even close!) but it is common enough that my high school math teacher used to refer to his best students as his "M & M students." Not because they liked chocolate in a candy shell, but because they excelled in both Math & Music.

So what's the connection? I'm going to suggest three connections: patterns, precision, and creativity.

Patterns in Music

Music is filled with patterns. That can be seen in the simplest of ways: a couple days ago I sat down with my five-year-old son and taught him a little bit about the piano. I showed him how to find the note C by looking for patterns. There are sets of three black keys, and there are sets of two black keys. C is any white key that comes right before a set of two black keys. From there, he could find any C on the keyboard. I showed him that the note names go from A to G, and then start over at A. From there, he could start at the low end of the keyboard and name every single white key on the piano. Patterns.

Eventually he will discover that there are certain intervals (major thirds, minor thirds, etc) that sound really nice together, and others that don't sound quite as nice. He'll discover that those intervals can be shifted up and down the keyboard by octaves, and then he'll discover that they can be shifted by other amounts, and the sound is just as nice. 

Musical compositions are also filled wtih patterns. Just listen to Vivaldi's Four Seasons, and you'll hear the same "figure" repeated throughout a movement. Starting on one note, and then on another note, then with some variations to the pattern, but always with a pattern that your ear catches and hangs on to. Some of the most memorable classical compositions are the ones that have memorable patterns that appear over and over (think of "dum-dum-dum-DUM" in Beethoven's fifth symphony, or the themes of Rossini's "The Barber of Seville" and "William Tell Overture" - and if you're not familiar with those two compositions, think of Bugs Bunny as a barber, or the Lone Ranger). 

Patterns crop up in more modern music as well - the pattern of verse-chorus-verse-chorus-bridge-chorus is one that gets repeated over and over again in popular music. Your brain processes those patterns even if you're not consciously aware of them.

As an added bonus: most of the patterns we notice in music have a mathematical reason why they exist. For example, an octave is an interval that sounds good because the frequencies of the notes are in a ratio of 1:2.

Patterns in Math

I'm not sure I even need to say that math is filled with patterns. It seems intuitively obvious. But let's consider just a couple things. First, I remember how fascinated I was when I first discovered the nine-times-table:

9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45...

...and so on. As the tens place increases by one, the ones place decreases by one, and in each case, the sum of the digits is 9. What a fascinating pattern.

Fibonacci was famous for discovering patterns, and exploring how they related to the natural world around us - for more on Fibonacci, you might want to consider this book, reviewed here by Book Scrounger: Blockhead: The Life of Fibonacci.

A couple days ago my son went for his yearly checkup, and his doctor commented that math learning at his age is all about finding patterns.

People who like looking for patterns will naturally be drawn to either math or music, or both.

Precision in Music

If you've ever taken music lessons, you understand this one. I remember, as a violin student, being expected to be very precise about a lot of things: how I hold the bow, how I hold the violin, where I put my fingers, how I draw the bow across the strings. And then I'd do scales over and over again, with my teacher telling me, "That C-sharp isn't sharp enough." or "Your bow is way down on the fingerboard." Getting good at playing a musical instrument requires a fairly stubborn and determined mindset to get it right. For a violin student, "getting it right" is sometimes a matter of a miniscule fraction of an inch one way or the other. 

So when you said that "math is technical," my response to that is: so is music! Students who can't master the technical aspects will not excel.

Precision in Math

The same stubborn, determined mindset that makes someone decide they're going to practice a D-major scale until they get it right is necessary for a good math student as well. In elementary school it's memorizing those math facts. Then it turns into more and more complicated processes (arithmetic algorithms, arithmetic operations on fractions), and eventually the student is faced with complex algebraic and even calculus problems. And good math students practice these over and over again (it's why those cruel and nasty math teachers assign homework; doing 20 math problems is like practicing your D-major scale over and over and over again). You don't get that kind of precision any other way.

People who have the determination to keep practicing things are more likely to excel in math or music, or both.

Creativity in Music

Eventually, every violin student who sticks with it long enough gets to the point where their teacher says, "Okay, it's time to learn about vibrato." What is vibrato? Vibrato is, according to one dictionary: "a rapid, slight variation in pitch in singing or playing some musical instruments, producing a stronger or richer tone." In a sense, vibrato is a breaking of the rules, because you've been trying desperately to play in tune, and now your teacher is giving you permission to play out of tune. In fact, your teacher is demanding that you play out of tune. In my mind, it was at that moment that I moved from parroting to interpretation. You are no longer at the mercy of the musical composition; the notes on the page become a vehicle for your own personal expression. And vibrato is just one thing - whatever musical instrument you play, as you advance, you will discover more and more that there are ways to express yourself through creative use of the technical skills you've acquired. You've become creative.

And, do I need to mention? Writing musical compositions is a wonderful task in creativity!

Creativity in Math

Really? Math is "creative"? Sure it is! Math is problem solving! Math is curiosity, and exploring beyond what is known. When I graduated from high school, on Class Night, my math teacher presented me with a our school's highest math award, and at the same time presented me with a notebook which contained every math problem I'd solved during my independent study math course that year. What's the big deal about that (you might ask)? The big deal is that every one of the problems I worked on that year was a problem I made up myself, or decided to challenge myself with. Whether it was proving the quadratic formula, deriving a formula for the inverse of an N x N matrix, developing my own theorems, or just posing mathematical questions to myself and trying to solve them, I spent the entire year being creative. And that creativity is what makes a mathematician. Being a good mathematician doesn't mean being able to multiply 324 x 16.9; that's just the precision practice (like learning a musical scale); being a good mathematician means being able to take those skills you've practiced, and put them to use in new  ways to solve problems you haven't solved yet.

When I have students who want to take my math classes as "honors level" classes, I expect problem solving from them; I expect them to take the things they've learned and put them to use in brand new ways that they've never thought of before. I expect them to combine two mathematical ideas that they've never used together before, and use them to develop a solution to a problem they didn't think they could solve. I expect them to get creative.

People who are willing to use the tedium of repeated practice to explore new ideas and new ways of doing things will excel at either math, or music, or both.

"There is geometry in the humming of the strings, there is music in the spacing of the spheres." ~ Pythagoras

"I hate converting degrees to radians and the other way. Degrees seem simpler why can't we just stick to that?"

Good question! Degrees have been around for a long time. There are varying theories about where the unit originated. Some suggest that 360 comes directly from the Babylonians' sexagesimal (base 60) system; 360 = 6 x 60.

Others suggest that 360 was chosen because it is (approximately) the number of days in a year. Thus, a degree is roughly the angle traversed by the earth in a single day.

One thing that is certainly true: in the days before calculators, having units based around highly composite number would have been convenient for division purposes. 360 is highly composite, having 24 factors. Look at it this way. If you wanted to divide a circle in half, thirds, fourths, fifths, sixth, eighths, tenths, twelfths, fifteenths, sixteenths (and many others) you could do so without having any decimals to deal with.

That's great, although having calculators makes that less important to mathematicians than it once was.

So that's where degrees came from. What about radians?

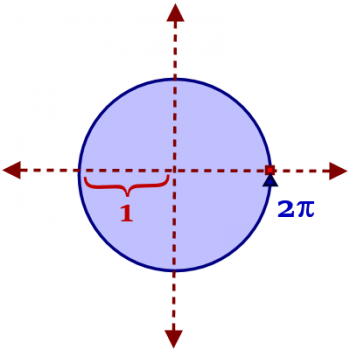
Radians come directly from a unit circle. When we talk about the unit circle, we're talking about a circle with radius 1, centered at the origin of the cartesian plane. If you look at the picture, you can see that the radius of the circle has been marked as 1 unit. Now look at the blue line, starting with the red beginning, and going all the way around the circle to the blue arrow. How long is that curved segment?

The answer to that question comes from the formula C = πd - the circumference is pi times the diameter. What is the diameter? It's twice the radius, or 2 x 1 = 2. Thus, the circumference is 2π. With that in mind, a rotation around the circle could be thought of as an arc-length around a unit circle.

Okay, so that's where radians come from - but it doesn't answer the question of why we use them. It does seem like 30º is easier to deal with than π/6, and 270º is easier to deal with than 3π/2. So why deal with radians at all?

Because, as you move through more advanced topics in mathematics, you'll discover that there are certain relationships that only work if you're using radians instead of degrees. Consider the infinite summation below:

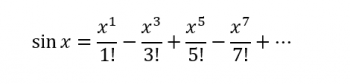
This beauty only works if x is in radians; if it's in degrees, it does not work!

But pretty formulas aren't the only reason radians work better. Especially if you're dealing with rotational motion (a car's tires, for example), writing things in radians keeps it simple. Consider the following examples:

#1: A car's tires have a radius of 12 inches. Its rotational speed is 30 degrees per second. How far does the car go in 1 second?

#2: A car's tires have a radius of 12 inches. Its rotational speed is 0.5326 radians per second. How far does the car go in 1 second?

#1 Solution: To find the distance the car has traveled, we divide 30 by 360 to find out what fraction of the circle we've rotated. Then we multiply that fraction by pi and the diameter of the circle to get the distance traveled: 12 x 2 x 30 x π / 360 = 6.3912 inches.

Now, before we look at problem #2, It's important to notice that in your calculations you've multiplied by 2π, and divided by 360. That's 2π/360, which is the same as π/180. That should look familiar to you; it's the conversion factor to swap from degrees to radians. In other words, even though you didn't realize you were doing it, you converted degress to radians in order to solve the problem! Now let's look at the solution to the second problem (which, by the way, is identical to the first, just using different units).

#2 Solution: To find the distance traveled, multiply the radius by the rotation in radians: 12 x 0.5326 = 6.3912 inches.

Wasn't that solution much simpler? You didn't have to do any conversion factors; you just multiplied the radius times the angle! That's pretty sweet!

So, yes, it's a nuisance to have two different units (just be glad you don't have to throw gradians into the mix!), but in the long run, your mathematical and scientific life will be simplified by making the π/180 switch to radians!

"How do you add 8 cubic yards and 8 cubic feet?" ~Anon.

Since you're asking the question, you're probably deduced that you can't simply add 3 and 3 to get 6. If you did that, you'd then have the question of whether the units in the result are cubic yards or cubic feet. The simple rule is that you can't add two quantities which have different units. 

If two units are the same type of unit (for example, they're both distances, or they're both times), then you can rewrite one of them so they have the same unit, and then you can add them.

In this case, both units are volumes, which is an amount of 3-dimensional space something takes up. We want to either convert 3 cubic yards into cubic feet, or we want to convert cubic feet into cubic yards. I'm going to convert cubic yards into cubic feet.

If you have 8 cubic yards, you can picture that as a cube. Conveniently, 8 = 2³, so you can picture it as a cube that has a width of 2 yards, a height of 2 yards, and length of 2 yards. Length times width times height = 2 yards x 2 yards x 2 yards = 8 yards³.

But we know how to convert 2 yards into feet; there are 3 feet in a yard. So it turns out that our cube's dimensions are 6 feet by 6 feet by 6 feet. So Length times width times height = 6 x 6 x 6 = 216 feet³.

Now that we have written both units in cubic feet, we can add them: 216 feet³ + 8 feet³ = 224 cubic feet.

That answers your question, but we've really only touched the surface of converting units - you can find a more detailed study unit here: Conversions factors and unit conversions. 

"I can find the LCM of two numbers (like the LCM of 32 and 20 is 160), but how do you find the LCM if there are variables (like 32x²y and 20y³)?"

Before addressing your question, I'd like you to think, for a minute, about how you find the LCM of two numbers. When you were in elementary school, you may have been taught to list multiples until you find one that matches:

32: 32, 64, 96, 128, 160
20: 20, 40, 60, 80, 100, 120, 140, 160

This is fine, and is probably one of the easiest ways for children to visualize what it means that a number is the least common multiple. But since you're talking about variables, you're ready to approach LCMs in a slightly different way. If you already do LCMs the way I'm going to show below, please bear with me while I review it.

When I want to find the LCM of two numbers, I generally start by doing a prime factorization of the two numbers. You can use a factor tree, or whatever method you've learned. I get the following result:

32 = 2⁵
20 = 2² · 5

With this factorization, finding the LCM is a cinch. First, the LCM must have both 2 and 5 as factors. Why? Because it's a multiple of numbers that have 2 or 5 (or both) as factors. So I can say:

LCM = 2^? · 5^?

What are those question marks for? They're there because even though I know the LCM has both 2 and 5 as factors, I haven't figured out what the exponents of those factors are. It's actually pretty simple to figure out, though; we compare the exponents of each factor in the two prime factorizations, and we take the larger exponent. Thus, since we have 2⁵ and 2², 5 is the bigger exponent, and since we've just got 5¹ in the second factorization, that's the exponent we'll use for 5.

LCM = 2⁵ · 5¹ = 160

Now, maybe you think that process is a lot slower than the other process. Maybe. Or maybe it just seemed that way because I was explaining each step. On the other hand, if you have the numbers 1008 and 1012, finding the LCM by the elementary method is going to be brutal (the result is 255024, and you'll have to list out 253 multiples of 1008 and 252 multiples of 1012). 

But whether or not it's "easier" isn't actually the point. The point is that this method helps us answer your question about LCMs involving variables.

What are the prime factorization of  32x²y and 20y³?

32x²y = 2⁵ · x² · y
20y³ = 2² · 5 · y³

So the LCM has to contain the factors 2, 5, x, and y. And which exponents do we use? The higher exponent for each factor:

LCM = 2⁵ · 5 · x² · y³ = 160x²y³.

As a bonus, this method also allows us to find the LCM of some polynomial expressions. For example, find the LCM of x² + 2x + 1 and x² + 3x + 2. As with the previous problems, we begin by factoring:

x² + 2x + 1 = (x + 1)²
x² + 3x + 2 = (x + 1)(x + 2)

What is the LCM? It's (x + 1)²(x + 2)

What is the "altitude to the hypotenuse," and how do I find its length, if I know the lengths of two legs?

To answer this question, consider the diagram below. I show a triangle with angles A, B, and C, and right angle at C. The segment CD is the altitude to the hypotenuse. An altitude is a line segment that is perpendicular to a side, and passes through the opposite vertex. Thus, the altitude to the hypotenuse is perpendicular to the hypotenuse, and passes through the point C.

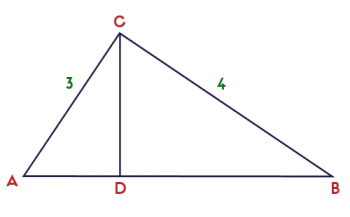
For this example, I gave the legs lengths 3 and 4. I did this so it would work out simply: the hypotenuse is 5 (because 3² + 4² = 5²).

The question is, how do we find the length of CD? To figure this out, it is helpful to notice that all three triangles are similar. 

ΔABC ~ ΔACD ~ ΔCBD 

From this, we know that the ratio of the longer leg to the hypotenuse is the same for each triangle.

In the largest triangle, that ratio is 4/5.  In the smallest triangle, that ratio is CD/3.

Thus, 4/5 = CD/3, which leads to CD = 12/5.