Ask Professor Puzzler
Do you have a question you would like to ask Professor Puzzler? Click here to ask your question!
A video has been floating around that talks about "fast thinking" and "slow thinking," and a simple three-question test that people who perform well on tend to do better on a lot of other tasks. Here are the three questions:

1. A baseball bat costs a dollar more than a baseball. Together they cost $1.10. What is the cost of the baseball?
2. If it takes 5 machines 5 minutes to make 5 widgets, how long would it take 100 machines to make 100 widgets?
3. In a lake, there is a patch of lily pads.Every day the patch doubles in size. If it takes 48 days for the patch to completely cover the lake, how long would it take to cover half the lake?
The video doesn't give answers or explain all the questions. Can you help?
I'll give it a go. But first, let me guess what the "fast thinking" (incorrect) answers are:
1. The ball costs ten cents.
2. It takes 100 minutes.
3. It takes 24 days.
Were those the answers you came up with? If they were, don't feel bad - these are the "natural" answers. But let's look at the real answers.
Baseball Problem
If b is the cost of the baseball, then the cost of the baseball bat is b + 1. This means that b + (b + 1) = $1.10. This leads us to 2b + 1 = 1.1, or 2b = .1. Dividing both sides by 2 gives us b = $0.05, or five cents. This is half of the instinctive response.
Widget Problem
You have 20 times as many machines, which means they can make 20 times as many widgets in five minutes. You know what that means, right? It takes 5 minutes! All 100 of those machines are working simultaneously, and each group of 5 machines makes 5 widgets in that five minutes. This is similar to the cat and mouse problem which can be found in our reference pages: Cat and Mouse Variation.
Lily Pad Problem
The correct answer to this is not half of 48; it's one less than 48. If the lake is half covered on one day, it'll be completely covered the next day. Therefore, it takes 47 days for the lake to be half covered.
What is the solution to the following puzzle that's been going around facebook?
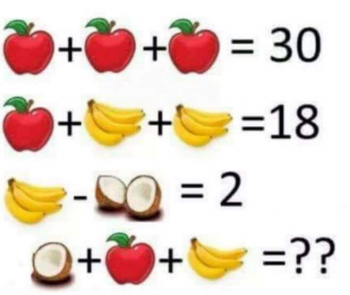
The answer is, on the surface, not terribly difficult to find:
3 apples = 30, so 1 apple = 10.
10 + 2 bananas = 18, so 2 bananas = 8 and 1 banana = 4
4 - 1 coconut = 2, so 1 coconut = 2
Therefore, 1 coconut + 1 apple + 1 banana = 2 + 10 + 4 = 16
HOWEVER...
Although this is the answer everyone seems to be giving, it's actually not correct. Notice that each bunch of bananas has four bananas (look closely!) except the one in the final line, which has 3 bananas. Also notice that the third line has one coconut, while the last line has only 1/2 of a coconut.
This changes things!
3 apples = 30, so 1 apple = 10.
10 + 8 bananas = 18, so 8 bananas = 8 and 1 banana = 1
4 - 1 coconut = 2, so 1 coconut = 2
Therefore, 1/2 coconut + 1 apple + 3 bananas = 1 + 10 + 3 = 14
This is a really nice problem, since it gives you a good reminder to pay attention to details!
Click the image below to read Professor Puzzler's analysis of another puzzle:

Addendums
William from Phoenix asks, "Apples coconuts bananas: The editing to remove the fourth banana was incomplete. it left the end point in the picture on line four. Was that intentional to cause controversy with your answers?"
Honestly, William, I can't see the incomplete erasure you're talking about. I don't doubt you, but I'm not seeing it. But, since you asked, I'll take this opportunity to point out: I didn't create this problem; I just wrote up the solution for people who wanted to know. If I had to make a guess, I would say that the person who created it did not intentionally leave part of a banana; they probably were just inexperienced with photoshop, or were in a hurry when they created it!
Colton from Florida had a question about the Algebra of this problem, which we answered here: Can X and Y have the same value?
Pany from UK points out that there is another way to interpret the problem, in which we regard each image as a symbolic variable, rather than as collections of real world objects. While I don't agree with him that this is the best way of looking at it, it is absolutely a valid way of viewing the problem, and it results in a very different problem, which is unsolvable, because we have more variables than equations. And speaking of which...
Anne from Maine shared with us a similar looking problem with a very different solution. Click the image below to read that post:

A visitor from India poses the following question: "You have five fives. 55555 now, (i) Arrange the fives to get largest possible value (ii) arrange the fives to get a value equal to 1. (iii) Arrange the fives to get a value less than 1. (iv) Arrange the fives to get a value equal to 56. remember : do not use the signs +.-,x,/ . But a bar or line between two digits can be helpful"
If you read my previous blog post on matchstick puzzles, you know that I don't expect there to be just one solution to this, and that anyone who thinks there is just one solution is probably being naive. Furthermore, this puzzle requires you to "think outside the box," and the person who gave you this puzzle may have a specific way they expected you to think outside the box, and therefore may not like your solutions.
I have solutions for all four parts.
They're probably not the solutions the problem poser was looking for.
And I'm not going to tell you my solutions.
Instead, I'm going to give you some pointers in directions that may help you solve the puzzle. I'll suggest to you some of the ways I "thought outside the box," and let you try to work through the possibilities to arrive at your own solutions (which might be different from mine!)
I also am not going to tell you which "outside the box" idea I used for which part of the puzzle. I don't want to give you too much help!
Ready? Here we go...
- First, I'd like to point out that your problem certainly has a typo in it. There are commas separating each of the symbols you can't use, except that between the plus and the minus, there is no comma - there is a period instead. This is certainly a typo, since the list is inconsistently displayed otherwise. This is important, because there are solutions available which make use of a decimal marker, and the decimal marker has NOT been eliminated in the rules. (If they had intended to eliminate the decimal point, they should have written: "do not use the signs +,.,-,x,/" There is no way to read their actual sentence that isn't grammatically nonsensical, so we'll make the assumption that the decimal point is allowed.)
- You have hopefully thought of using exponents, but have you thought of using exponents within exponents? Or even exponents within exponents within exponents? Something like this:

-
Although the forward slash (division symbol) has been eliminated from use, the horizontal fraction bar has not. In fact, the statement of the rules almost begs you to use the fraction bar.
- Speaking of bars, don't forget that a bar over a digit represents a repeating digit.
- Did you know that if you flip (not rotate) a five upside down, it's a two?
- Eliminating specific operators implies that anything not specifically eliminated is fair game. Have you ever run across the "bracket" operator? The brackets represent the operation "greatest integer of." If you see the expression [3.53], that evaluates to 3. Basically, you just drop the stuff after the decimal.
- Following along with my previous observation, the "factorial" operator has not been eliminated either, so you could do 5! if you wanted, and 5! = 5(4)(3)(2)(1) = 120.
Using just those ideas, you can come up with solutions for all four parts of this puzzle. Of course, if you take it back to the person who posed the puzzle in the first place, they may say something like, "But you're not allowed to flip the fives upside-down," or "You can't use the greatest integer function," or "You can't use a decimal point," or have some other lame excuse why your solution isn't the "correct" one.
Ask me if I care.
Nope. I don't. Thanks for asking. If they didn't want you to do certain things, they should have specified in the rules! :)
Good luck working out the rest of the puzzle. If you figure out some solutions, I'd love to hear back from you!
Professor Puzzler
The following blog post is an example problem designed to show why I don't answer peoples' "Matchstick Problems" on this blog. We've set up a new "Codes and Riddles" forum on our Community Forum, so you can share your matchstick riddles there and ask for help solving them. In order to post in the forum you must have a free membership account (click the login link at the top of the page to get started). We have an unusual "CAPTCHA" for the forum - instead of typing letters to prove you're human, we require you to solve at least 5 puzzles on the site before you post anything. (Here's a hint: Blackberry Game is about the simplest game on the site, so you can rack up your 5 games easily there!)
You wouldn't believe the number of times people have contacted me to ask me to solve a matchstick problem for them. You know the kind of problem I'm talking about, right? You're given a layout of matchsticks, and you are asked to move two (or one, or three, etc) matchsticks to form the largest number possible.
Here's an example: move 4 matchsticks to make the largest number possible out of the following:
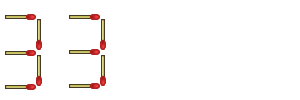
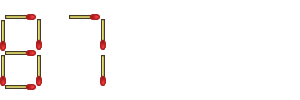
And to this second complaint, I reply, "Of course I moved four! I picked up two others and set them back down again!"
"That's not allowed," you say.
"Fine," I reply. "I didn't just set them down; I swapped them."
Here's a better solution, which, in a literal sense, thinks outside the box - instead of limiting myself to the two digits given, I expand the number to the right. This is a fairly obvious solution, and you shouldn't have any complaints about it:
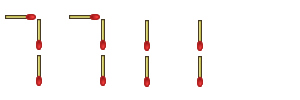
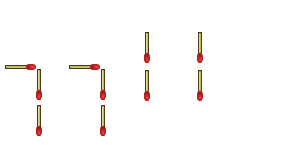
"There," I say, "that's about 500 quintillion - beat that!"
"You cheated! I never said you could use exponents!"
"And you never said I couldn't," I reply.
But wait! Who says a number one has to be two toothpicks tall? Aren't they still ones if they're made out of one matchstick apiece? Couldn't we do this:
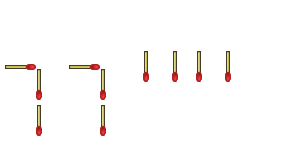
"Cheater!" someone declares, "You can't change the structure of the numbers!"
"I haven't changed the structure." I reply. "Exponents are supposed to be smaller, so I've formatted it perfectly."
Are we done yet? Are there more ways of thinking outside the box? Sure! Take a look at this one:
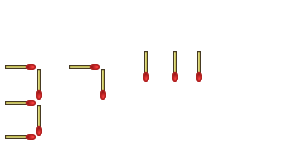
"Yeah, but you knew it was a seven, didn't you?"
"Besides," you protest, "you only moved three matchsticks - you couldn't have swapped two others, because that would have meant moving FIVE matchsticks"
"Ah," I say, glad to have you distracted from my malformed seven, "I picked up one that I wanted to move, and one that I didn't want to move, placed the one I wanted to move to the position of the one I didn't want to move, and then moved that one to the new position."
"Okay, fine!" you say, "You win!"
So what is that number? Well, we need to evaluate 7111 first, and that's 3.9e93, and when you try to raise 3 to that number, you're going to get an overflow error on your calculator.
And so I sit here smugly satisfied with myself - until someone else comes along and says, "Wait a minute! If you're going to let him get away with that malformed 7, then I can do this:"
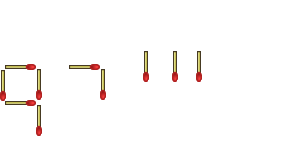
No! Even though I've come up with solutions that are too big to run through your calculator, this is just what I came up with on the spur of the moment - there are almost certainly better solutions out there! *
So what's the point? The point is twofold:
- Have fun with these kinds of problems, but if someone asks you one of these and doesn't clarify the rules of what you can and can't do, just have fun thinking outside the box, and when they say, "You can't do that!" enjoy the opportunity to annoy them with the response, "You never told me I couldn't!"
- If you ask me to solve your matchstick puzzle, I will simply direct you to this blog post, because I would almost certainly NOT come up with the solution the problem poser was looking for, so why should I even try - it's not MY puzzle after all! :D
Happy Puzzling!
Professor Puzzler
* Within a half an hour of posting this, two more even better solutions popped into my head - neither of which require malformed numbers. How many can you find that beat 9^(7^111)?


