Twelfth grader Jodi asks, "Hi Professor, if you could help me understand this problem I would highly appreciate it. Problem: An ant starts digging a tunnel. On the 1st day he digs 9m north. The 2nd day he digs 6 m east. The 3rd day he digs 4m south. He continues to dig in this pattern. Question 1: How far will he dig in total? Question 2: How far north from his starting point will he end up?"

Hi Jodi, this is definitely a fun problem. I'm going to answer these two questions, and then I'm going to pose two more questions for you to think about.

Question 1: How far will the ant dig?

Each day the ant digs 2/3 of what he dug the day before. Thus, his total distance is

Eq. 1: D = 9 + 6 + 4 + 8/3 + 16/9 + ...

Now, there are formulas you can use to calculate that sum, and if you're in a Pre-Calculus class (or higher) you probably know those formulas. I'm going to show you how to get that sum without a formula.  I'm going to take the equation and multiply it by 2/3:

Eq. 2: 2/3D = 6 + 4 + 8/3 + 16/9 + 32/27 + ...

Now, if I subtract the second equation from the first one, all but one of the terms on the right hand side of the equation cancel out, and  I get the following:

Eq. 3: D/3 = 9

This leads to D = 27, which is the answer to Question 1. If you want to make sure, pull out a calculator and punch in a bunch of these terms; you'll see that it doesn't take more than 7 or 8 terms for you to start getting close to 27.

Question 2: How far north from his starting point will he end up?

Before we get started, I'd like to point out that the problem seems just a tiny bit ambiguous. There are a couple ways I could read this:

1. The ant digs North, then East, then South, then repeats this pattern, going North, East, South, North, East, South, etc.
2. The ant digs North, then East, then South, then North, then West (completing the compass pattern) before repeating all four directions.

Strictly speaking, interpretation #1 is the precise reading of the problem, but I have a feeling interpretation #2 was intended, so I'm going to go with that one.

To solve this, we treat a distance south as a negative distance, and we look at the odd numbered terms of the original sequence (because the even numbered terms are east/west motions, and don't affect the north/south distance).

Eq 4: D_N = 9 - 4 + 16/9 - 64/81 + ...

This time the common ratio is negative (we know this because the terms are alternating signs). It is -4/9. So you can do the process I did above, multiplying the equation by -4/9 and then subtracting. Or you can use the formula I referred to above, but didn't tell you:

Eq 5: S = a/(1 - r), where a is the first term and r is the ratio.

D_N = 9/(1 - (-4/9)) = 9/(13/9) = 81/13

Question 3: What about the other digging pattern?

We made the assumption that the problem intended for the ant to dig in all four compass directions, but that may not have been the intent. What if the western direction is skipped each time? How does that affect the answer. It definitely makes it more interesting; I think you'll end up needing to treat it as two separate series: D_N and D_S, and then find the difference.

Question 4: What's the total displacement?

Displacement is a word we use a lot in Physics. It's different from the concept of distance (which is how far the ant traveled). Displacement is how far (and in what direction) the ant ended up from where he started, and it's a combination of the distance north, and the distance east. To find that answer, you would need to set up a D_E equation (distance east), and then do the Pythagorean Theorem on D_N and D_E to find the hypotenuse, which is the distance from his starting point to his ending point.

Since displacement is a vector (magnitude and direction) you'd also have to do a bit of trig to find the direction in which the ant ended up from his starting point.

Those are problems I'll leave you to contemplate. Thanks for asking!

Professor Puzzler

Akash from Surat asks, "There were 200 fishes in an aquarium, 99% of which were red. How many red fishes must be removed to make the percentage of red fishes 98%?"

Hi Akash, let's see if we can set up a solution for this one.

First of all, 99% of 200 is 198 red fish. (Because 200 x 0.99 is 198).

If we remove x red fish from the tank, we have 198 - x red fish left out of 200 - x total.

Thus, the equation we need is ^{(198 - x)}/_{(200 - x)} = 0.98.

198 - x = 0.98(200 - x)
198 - x = 196 - 0.98x
2 = 0.02x

x = 100 red fish removed.

Let's check our answer. If we remove 100 fish, and they're all red, we'll have 198 - 100 = 98 red fish, and a total of 200 - 100 = 100 fish.

Sure enough, 98 out of 100 is 98%.

It's tempting to think that if 198 fish is 99%, then 196 must be 98%, but that reasoning forgets that we aren't just decreasing the number of red fish; we're also decreasing the total number of fish!

Happy Valentine's Day, one day late! We hope you all had a wonderful day yesterday, no matter how (or if) you celebrated the day. For all of our online friends, I have the only Valentine's Day card you'll ever need for your mathematician friends.

It references counting principles in combinatoric mathematics, and in case you're not familiar with the notation, please allow me to explain.

Suppose you went to a pizza restaurant, and when you ordered your pizza, they told you, "You can choose from any of the following toppings: pepperoni, olives, hamburg, mushrooms, onions, ham, pineapple, or sausage. Of those, you must choose three toppings." (I know, what restaurant demands that you choose exactly three toppings?)

So how do you determine the number of possible pizzas? Well, the reasoning goes something like this:

1. I have eight ways to choose the first topping (because there are eight toppings available).
2. Once I've done that, I now have seven ways to choose the second topping (because I've already chosen one).
3. Now for my third topping, I have six choices.
4. That gives me 8 x 7 x 6 = 336 possibilities.
5. BUT WAIT A MINUTE! If I chose "pepperoni, olives and ham" - is that really any different from choosing "olives, ham, and pepperoni"?? No, it's not; it's the same pizza no matter what order I pick the toppings in. So I have to eliminate the repetitions.
6. It turns out the number of repetitions is 6. Why? Because you could put pepperoni in 3 positions, leaving 2 positions for olives, and then 1 position for ham. 3 x 2 x 1 = 6.
7. So we take the total number of possibilities (336) and, recognizing that every different pizza has been counted six times, we divide by 6: ³³⁶/₆ = 56. There are 56 different ways of choosing your pizza.

There's a nice way of representing the fact that we've got 8 things to choose from, aned we're choosing 3 of them, and it looks like this:

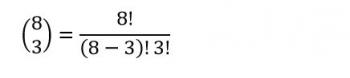
But how do we read that funny notation with the parentheses and two numbers inside of it? Since there are eight things, and we are choosing three, we read it as follows: "Eight choose three."

So, in honor of Valentine's Day, be sure to tell your favorite mathematician: 

One of my Pre-Cal students asked me a few days ago if the Law of Sines was hard to prove. I told him I'd write up a proof here. I also made my Pre-Cal class work through the proof themselves. I'll share their train of reasoning here.

First, we stated the Law of Sines:

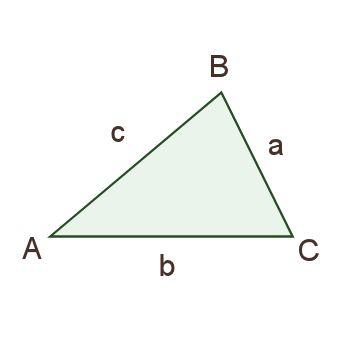
in triangle ABC, a/sinA = b/sinB = c/sincC.

They quickly recognized that we need a diagram to work from. So we drew something like the diagram to the right.

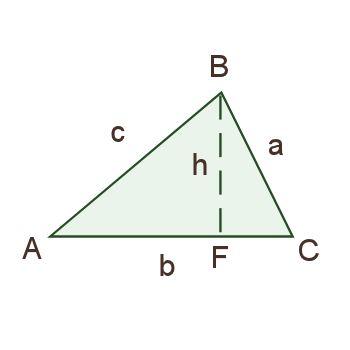
Then one of the students said, "Maybe we should draw in an altitude." Thus we had the following diagram. Their choice to label that new point F was somewhat random, I think, but I liked it, because F can stand for "foot" of the altitude.

After puzzling over their diagram for a bit, someone suggested setting up an equation involving the sine function and triangle ABF, and after a bit more thinking, a second equation involving the sine function and triangle CBF:

sinA = h/c; sinC = h/a.

They then did one of their favorite algebraic steps: multiplying both sides of an equation by a denominator in order to get rid of fractions (they don't like fractions, so they're always happy to get rid of them):

csinA = h; asinC = h.

A little substitution gives csinA = asinC. They then chose to divide both sides of this equation by sinAsinC, which gives:

c/sinC = a/sinA.

At this point, someone said, "Well we can just do this all over again with another side." Sure enough, if you drew an altitude to a different side, you'd get b/sinB = c/sinC (or b/sinB = a/sinA, depending on which altitude you drew).

Thus, a/sinA = b/sinB = c/sinC, and the Law of Sines is proved. Nice teamwork, class!

This question comes from one of my Pre-Cal students, who wants to know if there's a nice rule like the "sum and product" factoring rule, that works when the roots are complex numbers.

The sum-and-product method he's referring to is this:

If we have a quadratic x² + bx + c, and we can find two numbers (let's call them m and n) that add to b and multiply to c, then the quadratic factors into (x + m)(x + n). Here's an example:

Factor x² + 13x + 36.

In order to factor this, I look for two numbers that add to 13, and multiply to 36. Can you find them? I usually start by asking, "What are two numbers that multiply to 36?" The first pair I think of is 6 x 6. But 6 + 6 isn't 13, so that doesn't work. Next I think of 9 x 4. Aha! 9 + 4 is 13. So, since 9 x 4 = 36 and 9 x 4 = 13, I conclude that:

x² + 13x + 36 = (x + 4)(x + 9).

Okay, so now the question is, what if the quadratic factors with complex numbers? Is there a nice way of doing this factoring rule?

Let's start with an example:

x² - 4x + 5

If I knew that the factorization of this resulted in complex numbers, I would remember another rule, that complex roots come in pairs: if one root is a + bi, then the other is a - bi.

So, we look for two numbers such that:

(a + bi) + (a - bi) = -4
(a + bi)(a - bi) = 5

Simplifying these gives:

2a = -4, or a = -2
a² + b² = 5
4 + b² = 5
b² = 1
b = ⁺/_- 1

Therefore, this factors as follows:

x² - 4x + 5 = (x - 2 - i)(x - 2 + i) Multiply this out, and sure enough, it's true.

Let's try generalizing this a bit. Suppose the quadratic was x² + mx + n, and we wanted to find complex roots with the sum and product method.

(a + bi) + (a - bi) = m
(a + bi)(a - bi) = n

2a = m
a² + b² = n

a = m/2

m²/4 + b² = n
b = SQR(n - m²/4)

So let's take another example, and put our rule into practice.

x² + 6x + 13

a is half of 6, or 3.

b is SQR{13 - 6²/4) = SQR{13 - 9} = 2.

Therefore x² + 6x + 13 = (x +3 + 2i)(x + 3 - 2i).

This isn't too bad, but it presumes that the leading coefficient of the quadratic is 1; things might get a bit dicier if it wasn't. And, of course, if you're paying close attention, the result we obtain is actually just a slightly re-arranged version of the quadratic formula as it would appear in the special case of the leading coefficient being one!