Eleventh grade Max from England has a question for us, which references our Vortex Based Math pages:

"Hello prof! Lately I've been finding myself doodling little stars in the margins of my workbooks, seeing what patterns I can make with x number of points in a circle, a rule for arranging lines, making notation for different rules and so on. So far it's just been harmless messing around with patterns, but I saw your post on vortex maths and I'm concerned at the similarities I'm seeing with my own work. I don't think of myself as particularly 'mystic' but I do appreciate the patterns in mathematics, a la ViHart on YouTube and I'd rather not end up like Marko Rodin. My question is, should I keep on doodling and doing pseudo-mathematical patterns or move on and find something else? If so, what related things can I doodle that might bring me a bit closer to actual maths? Thanks for your time"

Well Max, I've got to tell you, this is one of the best questions I've seen in awhile. I like the way you're thinking. Before I answer your question, though I'm going to tell you a little story that your comment about doodling reminded me of.

When I was a kid, maybe in third or fourth grade, while all my classmates were learning addition and subtraction and the like, I was (I confess) a bit bored with math class.

So I started doodling. I doodled a tiny five-pointed star in the middle of my note paper. Then I drew a pentagon around it. Then I drew another star outside of that, and then another pentagon, and then another star, until my entire page was filled with stars within stars within stars.

And then I realized there was someone standing over my shoulder watching what I was doing.

It wasn't my teacher. Oh no, it was worse than that. It was the District Mathematics Curriculum Coordinator. And when you've been caught doodling by someone with such an impressive sounding title, it's a bit terrifying.

But Mr. Tame just asked me quietly, "What have you learned?"

I was a bit flustered (to say the least) but I had enough presence of mind to stumble out a response about how my first star wasn't perfectly drawn, and the more stars I drew, the more those errors got magnified.

He nodded thoughtfully and said, "That's a pretty important lesson," and then moved to look over the next student's shoulder.

I breathed a big sigh of relief and turned my attention back to addition and subtraction.

I appreciated Mr. Tame's willingness to let me get away with doodling. Because I did figure out something important about error and percent error (which I certainly could not have put into words at the time, but as Mr. Tame said, it was an important lesson).

So don't be afraid to doodle. Don't be afraid to explore. Don't be afraid of patterns. But don't stop just because you've found your pattern. Now ask the question, "Why?"  That's where Marko and his buddies fell apart. They thought the pattern was the end of the quest. But the pattern was just the beginning. From there they should have gone on to ask questions like, "What is the cause of these patterns?"

I love that you referenced ViHart. Have you watched her video about the golden ratio and Fibonacci numbers? If you haven't you should. There are some amazing, astounding patterns related to the Fibonacci sequence and the golden ratio that show up in nature. But ViHart doesn't just say, "Have you noticed that the leaves of a plant spiral in patterns related to Fibonacci numbers?" She says, "These are astounding patterns, and let's see if we can figure out why a plant's leaves tend to grow in this way!"

That's the difference between a Rodin and a ViHart. One is satisfied to find a pattern, the other wants to know why the pattern exists. Some of the most interesting mathematics and science stems from people discovering patterns and then trying to figure out why they happen.

A wise old king (Solomon) once said, "It is the glory of God to conceal a thing: but the honour of kings is to search out a matter." The universe is filled with extraordinary and beautiful patterns. They're like a buried treasure hidden just below the surface. But don't just find them. Dig them up. Search them out. Understand them.

And if you can't answer the question "Why?" Don't get discouraged. Go find something else to explore, and maybe someday down the road your explorations will connect some dots, and you'll have an answer to the question that you couldn't answer today!

Thanks for writing, Max!

Professor Puzzler

Michael from Los Angeles asks, "Let's say the first man, Adam did NOT eat the forbidden fruit. Then he would have procreated with Eve in the Garden of Eden and produced a family who would have procreated with each other to produce a bigger family who would have procreated with each other to have an even bigger family and on and on. How long would take for the population of this 'family' to reach, say, 5 million persons? Keep in mind these persons not only never die, they never age past 20 years physically. There is no sickness and they are ALL fertile at age 16. There is no pain assoiciated with child birth and every child is born perfectly healthy. Let's say they are equally male and female and begin to procreate at age 16 and, to make the math simpler, each couple only has one child per year. How long would it take for their number to equal 5 million?"

Well, Michael, once in awhile I get a question that interests me enough that I don't just answer it, I do additional exploration to amuse myself. And you're in luck, because I'm sharing my additional exploration with you.

You see, today while I was on my lunch break between teaching Algebra One and Algebra Two, I created a "population explosion simulator," which allows you to enter a variety of parameters, such as initial population, death age, number of years between child births, etc.

The default parameters for the simulator are the parameters which satisfy your question.

Population Explosion Simulator!

Enjoy!

Fifth grader Mario asks, "Is there a limit to the biggest or smallest Number?"

Good question, Mario! Sorry for the long delay in answering; we've been swamped with mail lately! The answer is: no, there's no limit. Numbers keep going on forever in all directions. You might not know the names of the numbers, but that doesn't mean they don't exist!

Big Numbers

What's the biggest number you can name? A million? A trillion? A quadrillion? A googol? (Not a Google, that's is a search engine!) A googol looks like this:

10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000

It's a pretty big number! (And it's also called ten duotrigintillion, but I don't even know how to pronounce that, so I'm going to stick to saying "googol.") A googol is a one followed by one hundred zeroes!

But is that the largest number? It isn't! After all, I could add one to it, couldn't I? Then I would have:

10 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 001

Better than that, I could multiply it by ten:

100 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000

Or by one hundred:

1 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000

Wait a minute! I could even multiply it by itself!

100 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000

I have no idea what to call that number (except I could call it "a googol times a googol"). But even though I don't have a fancy name for it, that doesn't mean it's not a real number, right? In fact, could I keep multiplying it by itself? Sure! I could even multiply it by itself a googol times, which would have so many zeroes that I couldn't possibly display it on this page.

No matter how big a number is, I can make it even bigger by tacking more zeroes on the end of it! So even though I don't know the names of all those numbers, there is no limit to how big a number can be!

Negative Numbers

When you said "how small" you might have meant a couple different things - you might have meant negative numbers, or you might have meant numbers close to zero. I'll address the question of how close you can get to zero in a second.

But first, in case you were talking about negative numbers, here's something you should know: For every positive number, there is a corresponding negative number. Take any positive number and stick a negative sign in front of it, and you've got the corresponding negative number. 7 and -7. 100 and -100. 1 googol and -1 googol. 

You get the idea, right? If there is no limit to how big the positive numbers can be, that means there's no limit to how big the negative numbers can be, either!

Close to Zero

But maybe, when you said "smallest number" you were talking about how close to zero you can get. And the answer is still "No, there is no limit."

For this, let's grab a calculator (if you have one handy) and check out a couple things. Calculate the following for me: 

• 1/2 = ?
• 1/3 = ?
• 1/4 = ?
• 1/5 = ?

These are called reciprocals. When you divide one by a number, you get that number's reciprocal. Many calculators have a reciprocal button; on my calculator it looks like this:

x^-1

You should get something that looks like this:

• 1/2 = 0.5
• 1/3 = 0.33333333
• 1/4 = 0.25
• 1/5 = 0.2

Notice that the bigger the number, the closer its reciprocal is to zero. Let's try a few more numbers to make sure. This time we'll pick numbers that are powers of ten (a one, followed by some zeroes).

• 1/10 = 0.1
• 1/100 = 0.01
• 1/1000 = 0.001
• 1/10000 = 0.0001

Oh, I'm seeing a definite pattern here! The number of zeroes after the decimal is one less than the number of zeroes in the number we took the reciprocal of. What happens if we divide 1 by a googol?  Well, you don't want to try to enter a googol in your calculator, but we can use the pattern to figure out the answer. (That just shows that you're actually smarter than a calculator!)

1/googol = 0.000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 1

Wow! That number is tiny! But is it the tiniest? No! Because there are numbers even bigger than a googol that we could take the reciprocal of. And the bigger the number, the closer its reciprocal is to zero! And since there is no limit to how big numbers can be, there's no limit to how close to zero we can get, either.

Another way of looking at it: No matter how close to zero a number is, we can always make it smaller by sticking another zero after the decimal point.

Now, Mario, when you get into high school or college, you'll probably take a calculus class, and you'll start learning more about these kinds of ideas. You'll start hearing teachers talk about "limits" and you'll think, "But wait! Long ago, Professor Puzzler told me there were no limits!" Don't worry. Keep listening. You'll realize that the way your teacher is using the term "limit" is different from the way you used it back when you were in fifth grade. And you'll also realize that we just scratched the surface of these ideas. When it comes to understanding math...

...the sky is the limit!

Vera from Michigan asks, "What is a star operation?"

First, let's talk for a second about operations in general. Operations are things that we can do to one or more expressions in order to create a new value from them. I say "one or more," because it's possible to have an operation that works on a single expression; we call that a unary operator. Most operations that you're familiar with take two expressions and combine them to make a new expression. We call these binary operators. In this blog post we'll talk about binary operators, and maybe someday I'll come back and do a blog post about unary operators.

What are some examples of binary operators? Multiplication is a good example:

3 x 5 = 15

In this example, we took two expressions (3 and 5) and we used the multiplication operator (x, or •) to combine them to create a new value:15. Now, you know that 3 x 5 = 15 because you memorized it at some point, but it wasn't just arbitrary memorization that got our result; the operation has a rule that gives you the result. The rule can be expressed in a few ways - here are just a couple:

• count to 3, five times. How many numbers did you count?
• create a rectangle that's 3 units wide and 5 units long. What is the area of the box in square units?

Every operation has a rule, or pattern, that we use to combine the two expressions into a single expression.

What are some other operators you're familiar with? Addition (+), subtraction (-), division (/).

But what is a star operation? Well, math teachers get bored, sometimes, with so few operations to confuse their students with, so they feel like inventing their own operations, complete with their own rules and their own symbols. Since the asterisk isn't used as an operation symbol (except in computer programming), we often use the asterisk as our operation symbol. Since the asterisk looks like a star, we dubbed it a "star operation." Let's look at an example:

Example One
We'll define our rule as follows a * b = a² + b².

This means that if we see something like 3 * 5, we'll plug the 3 in place of the a, and 5 in place of the b:

3 * 5 = 3² + 5² = 9 + 25 = 34.

Example Two
Rule: a * b = a(b - 1)

Find the value of 4 * 7.

In this case, we'll plug the 4 into our rule in place of a, and the 7 in place of the b:

4 * 7 = 4(7 - 1) = 4(6) =24.

By the way, it's interesting to note that our first example is commutative, which means that a * b = b * a, but the second rule is not. If we calculate 7 * 4 instead of 4 * 7, we don't get the same result:

7 * 4 = 7(4 - 1) = 7(3) = 21.

We don't have to use the asterisk symbol for our operation, by the way. We can pick any other unused symbol we want. It's not unusual to see a delta symbol (the Greek letter delta is a triangle with one vertex at the top) or an inverted delta symbol (pointing down instead of up), or a square, or a diamond, etc. We still often refer to them as star operations, even if they don't use the asterisk symbol.

Example Three
Rule: a ♦ b = (a + b)/2

Find the value of (2 ♦ 4) ♦ 6.

Notice that in this problem, we have parentheses, and our standard order of operations applies here - we have to evaluate the part in parentheses first:

2 ♦ 4 = (2 + 4)/2 = 6/2 = 3.

Now we evaluate 3 ♦ 6:

3 ♦ 6 = (3 + 6)/2 = 9/2 = 4.5.

As a side note, we observe that this operation is not associative; if we shift the parentheses, we get a different result: 2 ♦ (4 ♦ 6) = 3.5.

In closing, it can be fun to try to guess the rule for a star operation, given a table of values. Take a look at this example:

5 ¤ 3 = 16
7 ¤ 4 = 33
8 ¤ 6 = 28
8 ¤ 2 = 60

What do you think the rule could be? There could be more than one possible answer, and I'll leave it to you to figure it out. I'll give you one more equation to test your rule against:

1 ¤ 7 = -48

In my math classroom there hangs on the wall a poster I made, which looks something like this:

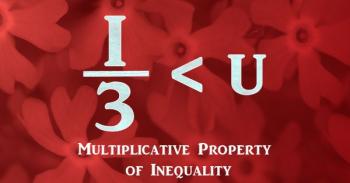
It usually takes quite awhile for my students to figure out the significance of the image. For one thing, they start out not knowing anything about the multiplicative property of inequality. When they ask me about it, I assure them that they'll learn over the course of the year a variety of properties of multiplication, and then they'll understand the poster.

What is the multiplicative property of inequality? The multiplicative property of inequality says that if you have an inequality, and you multiply both sides of the inequality by the same positive quantity, you will have an equivalent inequality. If you mutliply both sides by the same negative quanity, and change the direction of the inequality symbol, you still have an equivalent inequality.

Once my students understand this property, they look at the poster again, and since they all hate fractions, it doesn't take them long to decide they want to multiply both sides of the inequality by 3. This is a positive quantity, so they don't have to reverse the inequality sign. The result the obtain is:

I <3 U, which is an online shorthand for I love you (I - HEART - YOU).

Oh, those crazy, romantic, mathematicians!